您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“web分治算法怎么使用”,在日常操作中,相信很多人在web分治算法怎么使用問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”web分治算法怎么使用”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
在計算機科學中,分治法是一種很重要的算法。字面上的解釋是分而治之,就是把一個復雜的問題分成兩個或更多的相同或相似的子問題,再把子問題分成更小的子問題……直到最后子問題可以簡單的直接求解,原問題的解即子問題的解的合并。這個技巧是很多高效算法的基礎,如排序算法(快速排序,歸并排序),傅立葉變換(快速傅立葉變換)……
任何一個可以用計算機求解的問題所需的計算時間都與其規模有關。問題的規模越小,越容易直接求解,解題所需的計算時間也越少。例如,對于n個元素的排序問題,當n=1時,不需任何計算。n=2時,只要作一次比較即可排好序。n=3時只要作3次比較即可,…。而當n較大時,問題就不那么容易處理了。要想直接解決一個規模較大的問題,有時是相當困難的。
分治法的設計思想是:將一個難以直接解決的大問題,分割成一些規模較小的相同問題,以便各個擊破,分而治之。
分治策略是:對于一個規模為n的問題,若該問題可以容易地解決(比如說規模n較小)則直接解決,否則將其分解為k個規模較小的子問題,這些子問題互相獨立且與原問題形式相同,遞歸地解這些子問題,然后將各子問題的解合并得到原問題的解。這種算法設計策略叫做分治法。
如果原問題可分割成k個子問題,1<k≤n,且這些子問題都可解并可利用這些子問題的解求出原問題的解,那么這種分治法就是可行的。由分治法產生的子問題往往是原問題的較小模式,這就為使用遞歸技術提供了方便。在這種情況下,反復應用分治手段,可以使子問題與原問題類型一致而其規模卻不斷縮小,最終使子問題縮小到很容易直接求出其解。這自然導致遞歸過程的產生。分治與遞歸像一對孿生兄弟,經常同時應用在算法設計之中,并由此產生許多高效算法。
(1)二分搜索 (2)大整數乘法 (3)Strassen矩陣乘法 (4)棋盤覆蓋 (5)合并排序 (6)快速排序 (7)線性時間選擇 (8)最接近點對問題 (9)循環賽日程表 (10)漢諾塔
一、回文字符串
這里的回文是指資格字符串,它從頭到尾讀與從尾到頭讀的內容是一致的,比如說doggod,無論從左到右耗時從右到左都是一樣的。
def isPal(s): if len(s) <= 1: return True else: return s[0]==s[-1] and isPal(s[1:-1]) s = 'doggod' result = isPal(s) print result
二、二分查找
public static int binarySerach(int[] arr,int key){
int low = 0;
int high = arr.length - 1;
int middle = 0;
if(key < arr[low] || key > arr[high] || low > high){
return -1;
}
while(low <=high){
middle = (low + high)/2;
if(arr[middle] > key){
high = middle -1;
}
else if(arr[middle]< key){
low = middle + 1;
}
else {
return middle;
}
}
return -1;
}三、歸并排序
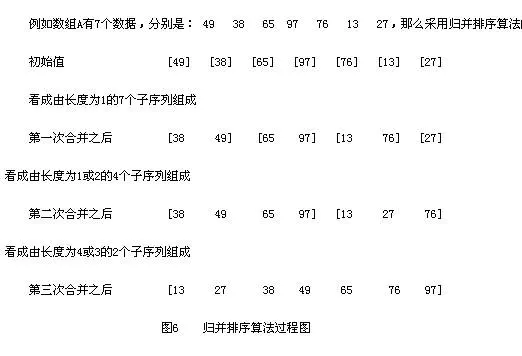
歸并排序(MERGE-SORT)是利用歸并的思想實現的排序方法,該算法采用經典的分治(divide-and-conquer)策略(分治法將問題分(divide)成一些小的問題然后遞歸求解,而治(conquer)的階段則將分的階段得到的各答案"修補"在一起,即分而治之)。
第一, 分解: 把待排序的 n 個元素的序列分解成兩個子序列, 每個子序列包括 n/2 個元素.
第二, 治理: 對每個子序列分別調用歸并排序MergeSort, 進行遞歸操作
第三, 合并: 合并兩個排好序的子序列,生成排序結果.
public static int[] sort(int[] a,int low,int high){
int mid = (low+high)/2;
if(low<high){
sort(a,low,mid);
sort(a,mid+1,high);
//左右歸并
merge(a,low,mid,high);
}
return a;
}
public static void merge(int[] a, int low, int mid, int high) {
int[] temp = new int[high-low+1];
int i= low;
int j = mid+1;
int k=0;
// 把較小的數先移到新數組中
while(i<=mid && j<=high){
if(a[i]<a[j]){
temp[k++] = a[i++];
}else{
temp[k++] = a[j++];
}
}
// 把左邊剩余的數移入數組
while(i<=mid){
temp[k++] = a[i++];
}
// 把右邊邊剩余的數移入數組
while(j<=high){
temp[k++] = a[j++];
}
// 把新數組中的數覆蓋nums數組
for(int x=0;x<temp.length;x++){
a[x+low] = temp[x];
}
}到此,關于“web分治算法怎么使用”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。