您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
最小二乘法擬合
最小二乘法(又稱最小平方法)是一種數學優化技術。它通過最小化誤差的平方和尋找數據的最佳函數匹配。利用最小二乘法可以簡便地求得未知的數據,并使得這些求得的數據與實際數據之間誤差的平方和為最小。
假設有一組實驗數據(x[i], y[i]),我們知道它們之間的函數關系:y = f(x),通過這些已知信息,需要確定函數中的一些參數項。例如,如果f是一個線型函數f(x) = k * x + b, 那么參數k和b就是我們需要確定的值。如果將這些參數組用p來表示的話, 那么我們就是需要找到一組p值使得如下公式中的S函數最小:
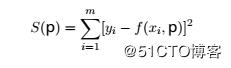
這種算法被稱為最小二乘法擬合。
scipy中的子函數庫optimize已經提供了實現最小二乘擬合算法的函數leastsq。下面是用leastsq進行數據擬合的一個例子。
import numpy as np
from scipy.optimize import leastsq
import pylab as pl
def func(x, p):
"""
數據擬合所用的函數:A * sin(2 * pi * k * x + theta)
"""
A, k, theta = p
return A * np.sin(2 * np.pi * k * x + theta)
def residuals(p, y, x):
"""
實驗數據x,y和擬合函數之間的差, p為擬合需要找到的系數
"""
return y - func(x, p)
x = np.linspace(0, -2 * np.pi, 100)
A, k, theta = 10, 0.34, np.pi / 6 #真實數據的函數參數
y0 = func(x, [A, k, theta]) #真實的y數據
y1 = y0 + 2 * np.random.randn(len(x)) #加入噪聲之后的數據
p0 = [7, 0.2, 0] #第一次猜測的擬合參數
#調用leastsq進行數據擬合
#residuals為計算誤差的函數
#p0為擬合參數的初始值
#args為需要擬合的實驗數據
plsq = leastsq(residuals, p0, args = (y1, x))
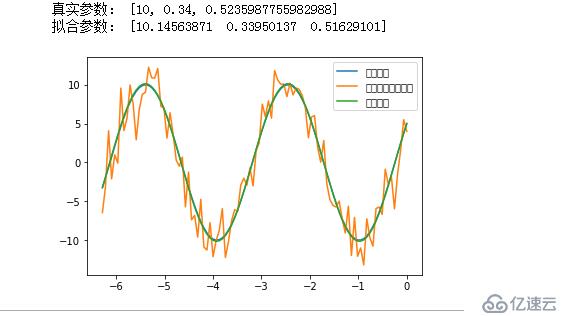
print("真實參數:", [A, k, theta])
print("擬合參數:", plsq[0]) #實驗數據擬合后的參數
pl.plot(x, y0, label = u"真實數據")
pl.plot(x, y1, label = u"帶噪聲的實驗數據")
pl.plot(x, func(x, plsq[0]), label =u"擬合數據")
pl.legend()
pl.show()
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。