您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
怎么用Python進行系統聚類分析,很多新手對此不是很清楚,為了幫助大家解決這個難題,下面小編將為大家詳細講解,有這方面需求的人可以來學習下,希望你能有所收獲。
在進行機器學習時,我們往往要對數據進行聚類分析,聚類,說白了就是把相似的樣品點/數據點進行歸類,相似度高的樣品點會放在一起,這樣一個樣本就會被分成幾類。而聚類分析也有很多種方法,比如分解法、加入法、有序樣品的聚類、模糊聚類法以及系統聚類法等。而本文要介紹的就是系統聚類法,以及如何用python來進行系統聚類分析。
首先來看一下系統聚類法的定義。系統聚類法(hierarchical clustering method),又叫分層聚類法,是目前最常用的聚類分析方法。其基本步驟如下:假設樣本中有n個樣品,那么就先將這n個樣品看作n類,也就是一個樣品一個類,然后將性質最接近的兩類合并為一個新的類,這樣就得到n-1個類,接著從中再找出最接近的兩個類,讓其進行合并,這樣就變為n-2個類,讓此過程持續進行下去,最后所有的樣品都歸為一類,把上述過程繪制成一張圖,這個圖就稱為聚類圖,從圖中再決定分為多少類。其大致過程如圖1所示。
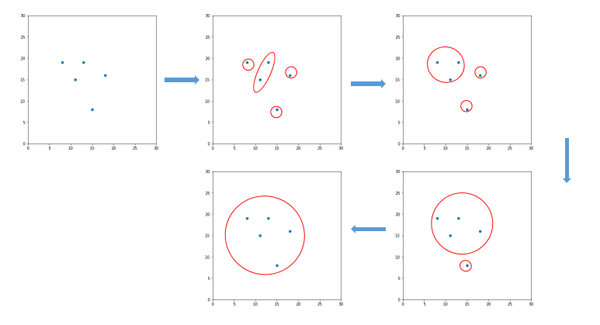
圖1. 系統聚類分析示意圖
而這里我們要確定各個樣品的相似度,才能將其歸類,那么如何確定其相似度呢?通常我們用的方法是計算各個樣品點之間的距離,然后再根據距離來分類。這里我們根據距離來分類,同樣也是有幾種方法的,比如最短距離法、最長距離法、重心法、類平均法以及ward法。下面我們對這幾種方法進行一個簡單的介紹。
1. 最短距離法
最短距離法就是從兩個類中找出距離最短的兩個樣品點,如圖2所示。點3和點7是類G1和類G2中距離最短的兩個點。計算公式如圖4所示。
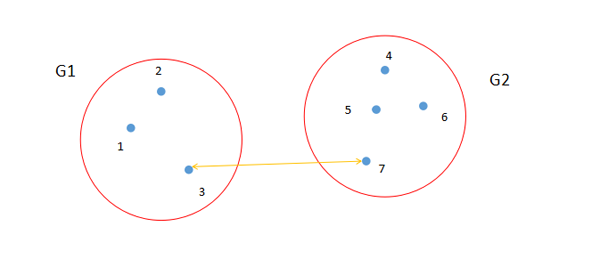
圖2. 最短距離法示意圖
2. 最長距離法
最長距離法就是從兩個類中找出距離最長的兩個樣品點,如圖3所示。點1和點6是類G1和類G2中距離最長的兩個點。計算公式如圖4所示。
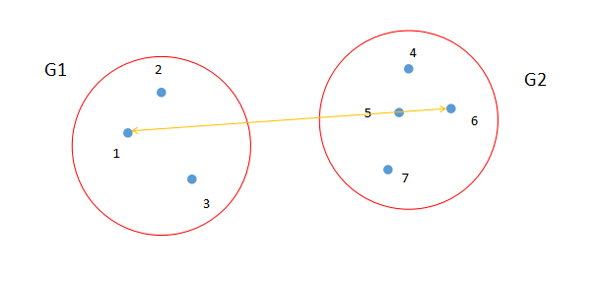
圖3. 最長距離法示意圖
3. 重心法
從物理的觀點看,一個類用它的重心,也就是類樣品的均值,來做代表比較合理,類之間的距離也就是重心之間的距離。若樣品之間用歐氏距離,設某一步將類G1與G2合并成G3,它們各有n1、n2、n3個樣品,其中n3=n1+n2,它們的重心用X1、X2和X3表示,則X3=1/n3(n1X1+n2X2)。重心法的計算公式參考圖4。
4. 類平均法
這個顧名思義,就是取兩個類之間所有點的距離的平均值。計算公式如圖4所示。

圖4. 常用的距離計算方法
5. 離差平方和法
離差平方和法又叫Ward法,其思想源于方差分析,即如果類分得正確,同類樣品的離差平方和應當較小,類與類之間的離差平方和應該較大。計算公式如圖4所示。
在了解了系統聚類法的基本知識以后,我們就用python代碼來展示一下系統聚類法的具體使用。
首先還是導入各種庫。
import numpy as np from matplotlib import pyplot as plt from scipy.cluster.hierarchy import dendrogram, linkage
接下來是生成數據集。我們這次用的數據集是隨機生成的,數量也不多,一共15個數據點,分為兩個數據簇,一個有7個數據點,另一個有8個。之所以把數據點數量設置這么少,是因為便于看清數據分布,以及后面畫圖時容易看清圖片的分類。代碼如下。
state = np.random.RandomState(99) #設置隨機狀態 a = state.multivariate_normal([10, 10], [[1, 3], [3, 11]], size=7) #生成多元正態變量 b = state.multivariate_normal([-10, -10], [[1, 3], [3, 11]], size=8) data = np.concatenate((a, b)) #把數據進行拼接
這里我們設置一個隨機狀態,便于重復試驗。然后利用這個隨機狀態生成兩個變量a和b,這兩個變量就是前面說過的數據簇,a有7個數據點,b有8個,a和b都是多元正態變量,其中a的均值向量是[10, 10],b的均值向量是[-10, -10],兩者協方差矩陣是[[1, 3], [3, 11]]。這里要注意的是協方差矩陣要是正定矩陣或半正定矩陣。然后對a與b進行拼接,得到變量data。
接下來要繪制數據點的分布。代碼如下。
fig, ax = plt.subplots(figsize=(8,8)) #設置圖片大小 ax.set_aspect('equal') #把兩坐標軸的比例設為相等 plt.scatter(data[:,0], data[:,1]) plt.ylim([-30,30]) #設置Y軸數值范圍 plt.xlim([-30,30]) plt.show()這里代碼比較簡單,不再贅述,主要說一下ax.set_aspect('equal')這行代碼,因為matplotlib默認情況下x軸和y軸的比例是不同的,也就是相同單位長度的線段,在顯示時長度是不一樣的,所以要把二者的比例設為一樣,這樣圖片看起來更協調更準確。所繪制圖片如圖5所示,從圖中可以明顯看到兩個數據簇,上面那個數據簇大概集中在坐標點[10, 10]附近,而下面那個大概集中在[-10, -10]附近,這和我們設置的是一樣的。從圖中可以很明顯看出,這個數據集大概可以分為兩類,即上面的數據簇分為一類,下面的數據簇分為另一類,但我們還要通過算法來計算一下。

圖5. 所用數據分布圖
然后是數據處理,代碼如下。
z = linkage(data, "average") #用average算法,即類平均法
數據處理只有這一行代碼,非常簡單,但難點也就在這。首先我們來看一下z的結果,如圖6所示。

圖6. 聚類計算結果
很多人第一次看到這個結果都是一臉懵逼,甚至是n臉懵逼,但其實里面的道理很簡單。scipy官方對此有一些設定,比如該結果中第一行有4個數字,即11、13、0.14740505、2,前兩個數字就是指“類”,剛開始每個點就是一個類,所以11和13這兩個點就是兩個類,第三個數字0.14740505就是這兩個點的距離,這兩個點被合并成一個類,所以這個新的類包含兩個點(11和13),這也就是第四個點的數值2,而這個新的類就被算為類15。注意這里是類15,不是第15個類,因為我們原來的數據集中有15個點,按照順序就是類0、類1、類2...類14,因為python是從0開始,所以這里類15就是指第16個類。z的第二行數據里,前兩個數字是2和5,就是原來類2和類5,距離是0.3131184,包含2個點,這行數據和第一行類似。然后再看第三行數據,前兩個數字是10和15,就是類10與類15,類15就是前面第一行合并成的新類,其包含11和13這兩個點,類15與類10的距離是0.39165998,這個數字是類11和13與類10的平均距離,因為我們這里用的算法是average,類10、11和13合并為了一個新類,其包含3個點,所以第四個數字就是3。z中其他行的數據按照此規律以此類推。最后一行數據中,類26和27合并成一個新類,這個類包含了全部15個點,也就是這15個點最終劃為了一個類,算法終止。
接下來就是畫圖,代碼如下,其結果如圖7所示。
fig, ax = plt.subplots(figsize=(8,8)) dendrogram(z, leaf_font_size=14) #畫圖 plt.title("Hierachial Clustering Dendrogram") plt.xlabel("Cluster label") plt.ylabel("Distance") plt.axhline(y=10) #畫一條分類線 plt.show()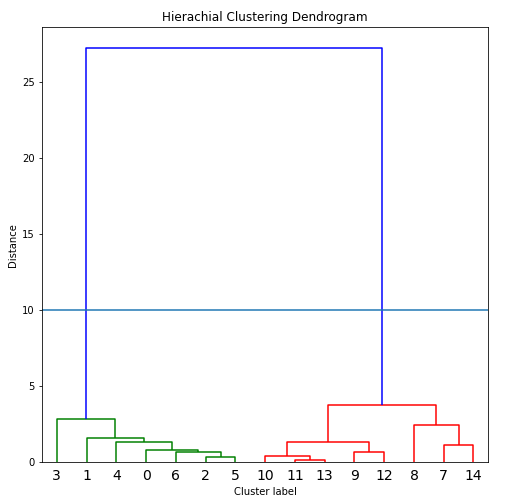
圖7. 聚類結果圖
從圖中可以看出,這15個點可以分為兩類,前面綠色的線連接的點代表一類,即點0到點6這7個點,后面紅色的線連接的點代表第二類,即點7到點14這8個點。我們可以看到這個劃分結果是非常正確的,和我們當時的設定是一樣的。
系統聚類法的算法比較簡單,實用性非常高,是目前使用最廣泛的聚類方法,但該方法在處理極大數據量時會有所不足,所以最好配合其他算法來使用,同時使用者在使用時要根據自己的情況,來選擇合適的距離計算方法。本文主要用類平均法來進行聚類操作,因為這個數據集非常簡單,所以用其他距離計算方法得到的結果和這個是一樣的。如果數據量比較大時,最終不同距離計算方法得到的結果可能不同,所以使用者要根據自己的情況來進行選擇。
看完上述內容是否對您有幫助呢?如果還想對相關知識有進一步的了解或閱讀更多相關文章,請關注億速云行業資訊頻道,感謝您對億速云的支持。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。