怎么理解二叉樹

本篇文章為大家展示了怎么理解二叉樹，內容簡明扼要并且容易理解，絕對能使你眼前一亮，通過這篇文章的詳細介紹希望你能有所收獲。

大白話講解二叉樹

比如現在有個數組，存放了很多用戶的名字，需要從這個數組中找到包含指定的用戶名，最快的方式是什么?

我們會想到二分查找，雖然這種方式很快，但要達到最快還需要有個條件：數組有序。

如果我們能把插入用戶名的時候直接給他排序，那最后的結構就是有序結構。

因此有人設計了一種數據結構：二叉查找樹，也叫做二叉樹。

如下圖所示：這是一種二叉樹結構。

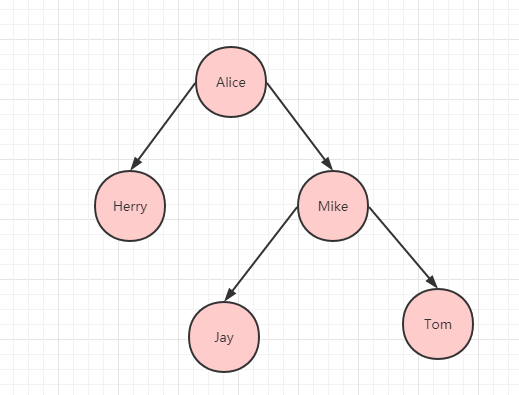
二叉樹

根據上文中的例子的，假定 Herry 在最上面，下面有  Alice，Mike，Ivy，Tom，從左到右，從上到下來看的話，最后的排序是：Alice->Herry->Ivy->Mike->Tom，確實是按照字母順序排的。

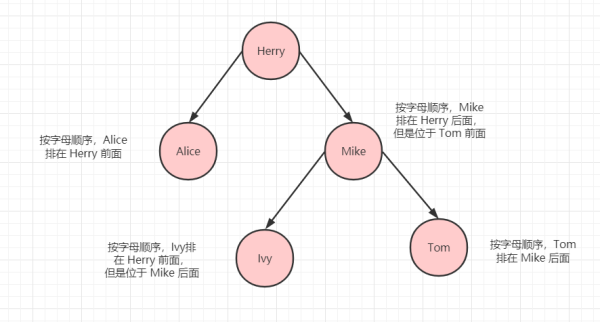
名字排序說明

其中有四個術語需要說明：節點、左節點、右節點、根節點。

其中每個紅色圓球都算一個節點，節點左下邊相連接的節點叫做左節點，而右邊相連的叫做右節點。比如 Alice 被稱作 Herry 節點的左節點，Mike  被稱作 Herry 的右節點。而根節點只會有一個，屬于最上面的節點，上圖中的 Herry 就是根節點。

對于其中每個節點，左子節點的值都比它小，而右子節點的值都比它大。比如 Alice < Herry < Mike。

假設現在我們想要查找 Ivy，首先檢查根節點，發現比 Herry 大，所以往下繼續找，找到了根節點的右節點 Mike，再繼續找，比 Mike 小，所以找  Mike 的左節點，正好找到 Ivy。

二叉查找樹中查找節點時，平均運行時間是 O(logn)，最糟糕的情況下所需時間為 O(n); 而在有序數組中查找時，及時最糟糕的情況，二分查找最多也是  O(logn)，所以你可能會覺得，二分查找比二叉查找要快很多。但是二叉查找樹的插入和刪除操作的速度是要快很多的。這里我們做一個對比：

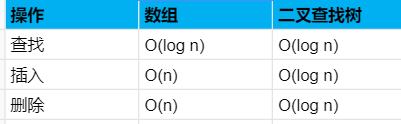
二叉樹與二分查找算法對比

但是二叉樹也有缺點：

• 不能隨機訪問。比如想要查找第 10 個元素，是不能返回第十個元素的，但是數組就可以通過下標索引找到。

• 二叉樹存在不平衡的情況，比如以根節點為中間的界限，發現右邊的節點數遠超左邊的節點數，那么左右不平衡，查找的效率就很低了。如下圖所示：

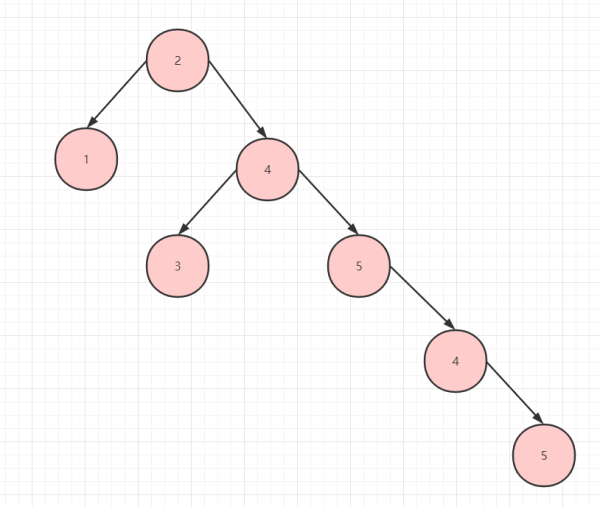
右邊節點數遠大于左邊節點數

那有沒有平衡的二叉樹呢?當然有，那就是紅黑樹，限于篇幅和側重點，這個放到下篇再講吧

二叉樹中的含義

二叉樹定義

大白話說二叉樹就是每個節點只能有兩顆子樹，且有左右之分。

來看看專業定義：二叉樹是 n(n>=0 )  個結點的有限集合，該集合或者為空集(稱為空二叉樹)，或者由一個根結點和兩棵互不相交的、分別稱為根結點的左子樹和右子樹組成。

二叉樹有 5 種形態

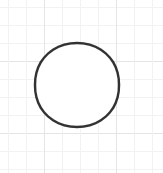
空二叉樹。

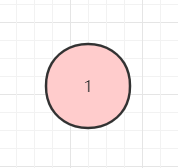
只有一個根節點的二叉樹。

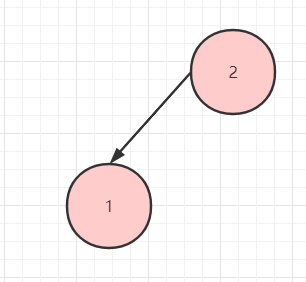
只有左子樹

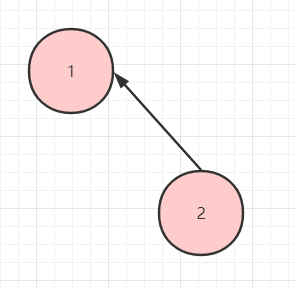
只有右子樹。

完全二叉樹。

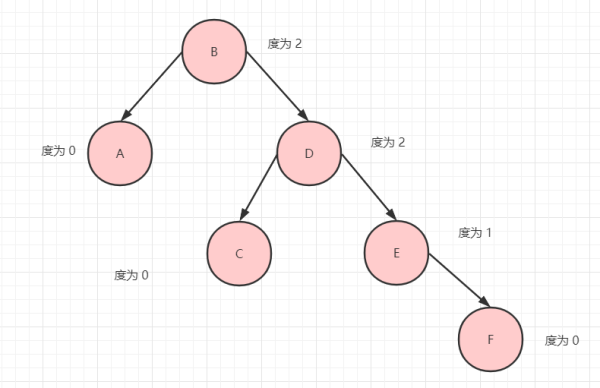
節點的度

定義：節點擁有的子樹數目稱為節點的度。

我們來看下圖就一目了然了。

mark

比如節點 B 的度為 2，節點 E 的度 為 1.

而樹的度就是所有節點的度的最大值，也就是 2。

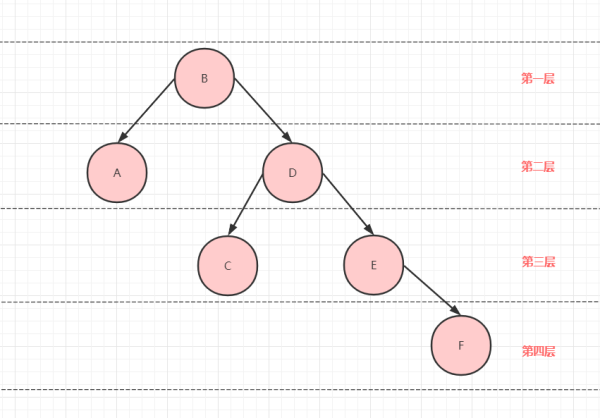
節點層次

如下圖所示：根節點為第一層，依次類推。

二叉樹的特點

每個節點最多有顆子樹，所以二叉樹中不存在度大于 2 的節點。

左右子樹是有順序的，次序不能任意顛倒。

即使某個節點只有一顆子樹，也是需要區分它是左子樹還是右子樹。

二叉樹的遍歷

二叉樹的遍歷：從二叉樹的根節點出發，按照某種次序依次訪問二叉樹中的所有節點，使得每個節點都能被訪問一次，且僅被訪問一次。

二叉樹的訪問次序可以分為四種：

• 前序遍歷。

• 中序遍歷。

• 后續遍歷。

• 層序遍歷。

前序遍歷：通俗的說就是從二叉樹的根結點出發，當第一次到達結點時就輸出結點數據，按照先向左再向右的方向訪問。

中序遍歷：就是從二叉樹的根結點出發，當第二次到達結點時就輸出結點數據，按照先向左再向右的方向訪問。

后序遍歷：就是從二叉樹的根結點出發，當第三次到達結點時就輸出結點數據，按照先向左再向右的方向訪問。

層次遍歷：就是按照樹的層次自上而下的遍歷二叉樹。

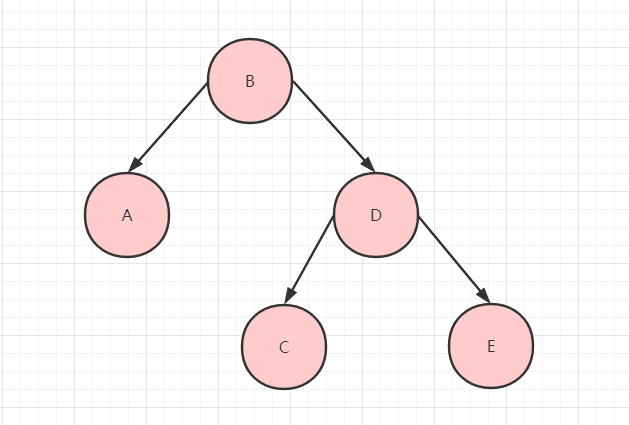
mark

按照前序遍歷的結果就是 BADCE。

按照中序遍歷的結果就是 ABCDE。

按照后續遍歷的結果就是 ACEDB。

按照層次遍歷的結果就是 BADCE。

上述內容就是怎么理解二叉樹，你們學到知識或技能了嗎？如果還想學到更多技能或者豐富自己的知識儲備，歡迎關注億速云行業資訊頻道。