如何使用LeetCode二叉樹

這篇文章主要講解了“如何使用LeetCode二叉樹”，文中的講解內容簡單清晰，易于學習與理解，下面請大家跟著小編的思路慢慢深入，一起來研究和學習“如何使用LeetCode二叉樹”吧！

樹

首先看看什么是樹??。

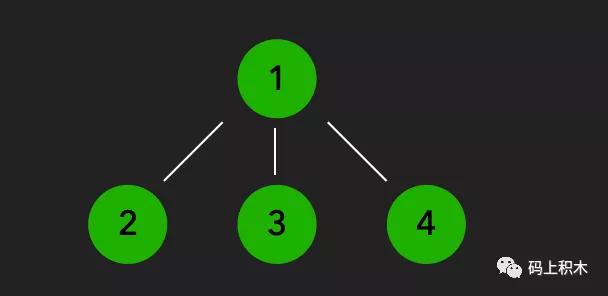
如圖，這種有節點的結構就是樹。

樹 是n(n>=0)個結點的有限集

其中：

• 每個元素叫做 節點

• 上一節是下一節的 父節點，比如1是2的父節點

• 最上面的節點，也就是沒有父節點的節點叫做 根節點，比如1

• 同一個父節點的節點叫做 兄弟節點，比如2、3、4是兄弟節點

• 沒有子節點的節點叫做 葉子節點

二叉樹

聽名字還是比較好理解的，就是每個節點有兩個分叉的樹。但是又不要求一定有兩個節點，只要小于等于2個節點就可以。

比如這種：

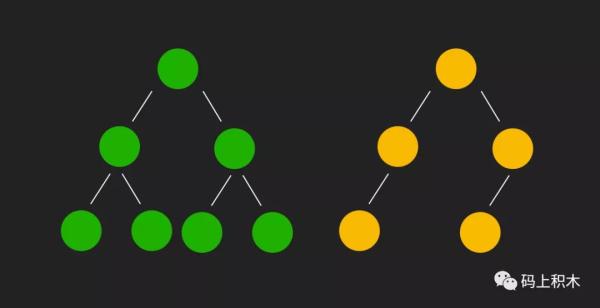
其中，可以看到綠色的樹每個節點都有左右兩個節點，這種二叉樹就叫做 滿二叉樹。

還有一種二叉樹叫做 完全二叉樹。

完全二叉樹:  對一顆具有n個結點的二叉樹按層編號，如果編號為i(1<=i<=n)的結點與同樣深度的滿二叉樹中編號為i的結點在二叉樹中位置完全相同，則這棵二叉樹稱為完全二叉樹。

啥意思呢，比如一個滿二叉樹，每個節點進行順序編號，如果去了一些節點，編號不會變化，那么就是完全二叉樹，比如：

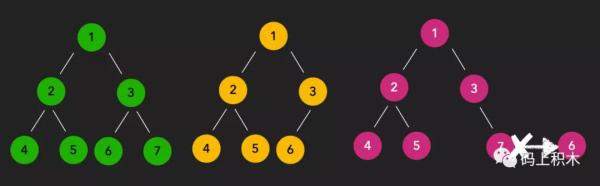
這張圖中，綠色樹是滿二叉樹，當去掉7號節點，變成了黃色樹。

這顆黃色樹的序號相對于滿二叉樹的序號都能一一對應，所以這個黃色樹就是完全二叉樹。

如果去掉的是6號節點，變成紅色樹，這時候，紅色樹的節點就必須有所變化了，6消失后節點7必須變成節點6才正確。

所以這個紅色樹就不是完全二叉樹，因為它相對于滿二叉樹序號有所改變，已經對應不上了。

算法&mdash;&mdash;平衡二叉樹

說了這么多，該來個題練練手了。

輸入一棵二叉樹的根節點，判斷該樹是不是平衡二叉樹。如果某二叉樹中任意節點的左右子樹的深度相差不超過1，那么它就是一棵平衡二叉樹。

示例 1: 給定二叉樹 [3,9,20,null,null,15,7]

  3  / \ 9  20   /  \  15   7

返回 true 。

解析

題目給出了平衡二叉樹的概念，就是任意節點的左右子樹相差不超過1，就是平衡二叉樹。

那這個深度是啥呢?

深度就是根節點到當前節點經過的邊個數

層數就是當前節點在第幾層，跟節點為第一層，所以層數=深度+1

 1       深度 0 ，層數 1  / \ 2  3      深度 1 ，層數 2   /  \  4    5   深度 2 ，層數 3

解法1

首先容易想到的就是把每個節點的深度都算出來，然后進行左右節點比較就能得出是不是平衡二叉樹。

那么節點的子樹深度怎么計算呢?

遞歸。當子節點為空就返回，否則每次增加一個單位深度。

/**  * Definition for a binary tree node.  * public class TreeNode {  *     int val;  *     TreeNode left;  *     TreeNode right;  *     TreeNode(int x) { val = x; }  * }  */      private int depth(TreeNode root) {         if (root == null) return 0;         return Math.max(depth(root.left), depth(root.right)) + 1;     }

深度搞定了，這題就好解了，即遍歷每個節點的左右深度，還是要 用到遞歸：

class Solution {     public boolean isBalanced(TreeNode root) {         if (root == null) return true;         return Math.abs(depth(root.left) - depth(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);     }      private int depth(TreeNode root) {         if (root == null) return 0;         return Math.max(depth(root.left), depth(root.right)) + 1;     } }

從根節點開始，計算每個左子樹深度和右子樹深度的差值，以及下面的每個節點的左子樹和右子樹深度，最終得出結果。

這種先處理節點，在處理左子樹，再處理右子樹 的遍歷方式叫做 前序遍歷或者先序遍歷。

時間復雜度

假設節點總數為n，層數為x，二叉樹為滿二叉樹。

時間復雜度計算可以通過 每層的時間復雜度 * 層數復雜度

每層的時間復雜度：

• 第一層需要遍歷n次，第二層需要遍歷n-1次，第三層需要遍歷n-3次，所以每層的時間復雜度為O(n)

層數復雜度：

• 第一層為1個節點，第二層為2個節點，第三層為4個節點，第x層為2的x-1次方。

借助公式：

n >= 1+2+4+8+...+2^(x-2)+1 n <= 1+2+4+8+...+2^(L-2)+2^(L-1)

計算：

n >= 1+2+4+8+...+2^(x-2)+1 n >= (2^(x-1)-1) + 1  n >= 2^(x-1) x <= log2n+1

同理：

x >= log2(n+1)

所以一個接近平衡二叉樹的高度(層數)接近logn。

所以總的時間復雜度就是 O(nlogn)

空間復雜度

由于用到了遞歸，用到了堆棧幀，之前說過和最大遞歸深度成正比，所以空間復雜度為O(n)

解法2

還有沒有更好的解呢?

剛才我們用到的是先序遍歷，但是可以發現，每個節點都會計算一遍深度，會有大量重復計算，所以我們可以試試不重復的算法?比如直接后序遍歷。

后序遍歷：對于任意節點來說，先處理左子樹，再處理右子樹，最后再處理節點本身。

計算深度還是用到剛才的方法：

private int depth(TreeNode root) {       if (root == null) return 0;       int left = recur(root.left);       int right = recur(root.right);       return Math.max(left, right) + 1;   }

如果能計算左子樹深度和右子樹深度，那么我們可以直接進行比較，如果發現某個節點的左子樹深度和右子樹深度相差大于1，那么就可以直接返回false了。

所以綜合能得出解法二：

class Solution {     public boolean isBalanced(TreeNode root) {         return recur(root) != -1;     }      private int recur(TreeNode root) {         if (root == null) return 0;         int left = recur(root.left);         if(left == -1) return -1;         int right = recur(root.right);         if(right == -1) return -1;         return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;     } }

時間復雜度

n為總節點，遍歷所有節點，所以時間復雜度為O(n)

空間復雜度

O(n)

感謝各位的閱讀，以上就是“如何使用LeetCode二叉樹”的內容了，經過本文的學習后，相信大家對如何使用LeetCode二叉樹這一問題有了更深刻的體會，具體使用情況還需要大家實踐驗證。這里是億速云，小編將為大家推送更多相關知識點的文章，歡迎關注！