您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“什么是遞歸算法”,在日常操作中,相信很多人在什么是遞歸算法問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”什么是遞歸算法”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
先來看一下求斐波那契數的遞歸寫法。
int fibonacci(int i) { if(i <= 0) return 0; if(i == 1) return 1; return fibonacci(i-1) + fibonacci(i-2); }對于遞歸算法來說,代碼一般都比較簡短,從算法邏輯上看,所用的存儲空間也非常少,但運行時需要內存可不見得會少。
來看看這個求斐波那契的遞歸算法的時間復雜度是多少呢?
在講解遞歸時間復雜度的時候,我們提到了遞歸算法的時間復雜度本質上是要看: 遞歸的次數 * 每次遞歸的時間復雜度。
可以看出上面的代碼每次遞歸都是O(1)的操作。再來看遞歸了多少次,這里將i為5作為輸入的遞歸過程 抽象成一顆遞歸樹,如圖:
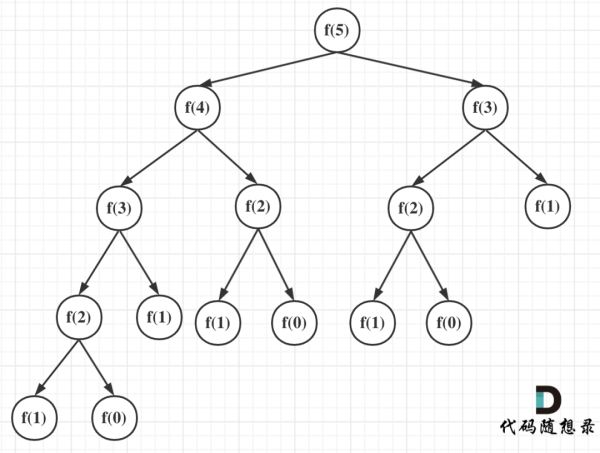
從圖中,可以看出f(5)是由f(4)和f(3)相加而來,那么f(4)是由f(3)和f(2)相加而來 以此類推。
在這顆二叉樹中每一個節點都是一次遞歸,那么這棵樹有多少個節點呢?
我們之前也有說到,一棵深度(按根節點深度為1)為k的二叉樹最多可以有 2^k - 1 個節點。
所以該遞歸算法的時間復雜度為 O(2^n) ,這個復雜度是非常大的,隨著n的增大,耗時是指數上升的。
來做一個實驗,大家可以有一個直觀的感受。
以下為C++代碼,來測一下,讓我們輸入n的時候,這段遞歸求斐波那契代碼的耗時。
#include <iostream> #include <chrono> #include <thread> using namespace std; using namespace chrono; int fibonacci(int i) { if(i <= 0) return 0; if(i == 1) return 1; return fibonacci(i - 1) + fibonacci(i - 2); } void time_consumption() { int n; while (cin >> n) { milliseconds start_time = duration_cast<milliseconds >( system_clock::now().time_since_epoch() ); fibonacci(n); milliseconds end_time = duration_cast<milliseconds >( system_clock::now().time_since_epoch() ); cout << milliseconds(end_time).count() - milliseconds(start_time).count() <<" ms"<< endl; } } int main() { time_consumption(); return 0; }根據以上代碼,給出幾組實驗數據:
測試電腦以2015版MacPro為例,CPU配置:2.7 GHz Dual-Core Intel Core i5
測試數據如下:
n = 40,耗時:837 ms
n = 50,耗時:110306 ms
可以看出,O(2^n)這種指數級別的復雜度是非常大的。
所以這種求斐波那契數的算法看似簡潔,其實時間復雜度非常高,一般不推薦這樣來實現斐波那契。
其實罪魁禍首就是這里的兩次遞歸,導致了時間復雜度以指數上升。
return fibonacci(i-1) + fibonacci(i-2);
可不可以優化一下這個遞歸算法呢。主要是減少遞歸的調用次數。
來看一下如下代碼:
// 版本二 int fibonacci(int first, int second, int n) { if (n <= 0) { return 0; } if (n < 3) { return 1; } else if (n == 3) { return first + second; } else { return fibonacci(second, first + second, n - 1); } }這里相當于用first和second來記錄當前相加的兩個數值,此時就不用兩次遞歸了。
因為每次遞歸的時候n減1,即只是遞歸了n次,所以時間復雜度是 O(n)。
同理遞歸的深度依然是n,每次遞歸所需的空間也是常數,所以空間復雜度依然是O(n)。
代碼(版本二)的復雜度如下:
時間復雜度:O(n)
空間復雜度:O(n)
此時再來測一下耗時情況驗證一下:
#include <iostream> #include <chrono> #include <thread> using namespace std; using namespace chrono; int fibonacci_3(int first, int second, int n) { if (n <= 0) { return 0; } if (n < 3) { return 1; } else if (n == 3) { return first + second; } else { return fibonacci_3(second, first + second, n - 1); } } void time_consumption() { int n; while (cin >> n) { milliseconds start_time = duration_cast<milliseconds >( system_clock::now().time_since_epoch() ); fibonacci_3(0, 1, n); milliseconds end_time = duration_cast<milliseconds >( system_clock::now().time_since_epoch() ); cout << milliseconds(end_time).count() - milliseconds(start_time).count() <<" ms"<< endl; } } int main() { time_consumption(); return 0; }測試數據如下:
n = 40,耗時:0 ms
n = 50,耗時:0 ms
大家此時應該可以看出差距了!!
說完了這段遞歸代碼的時間復雜度,再看看如何求其空間復雜度呢,這里給大家提供一個公式:遞歸算法的空間復雜度 = 每次遞歸的空間復雜度 * 遞歸深度
為什么要求遞歸的深度呢?
因為每次遞歸所需的空間都被壓到調用棧里(這是內存管理里面的數據結構,和算法里的棧原理是一樣的),一次遞歸結束,這個棧就是就是把本次遞歸的數據彈出去。所以這個棧最大的長度就是遞歸的深度。
此時可以分析這段遞歸的空間復雜度,從代碼中可以看出每次遞歸所需要的空間大小都是一樣的,所以每次遞歸中需要的空間是一個常量,并不會隨著n的變化而變化,每次遞歸的空間復雜度就是O(1)。
在看遞歸的深度是多少呢?如圖所示:
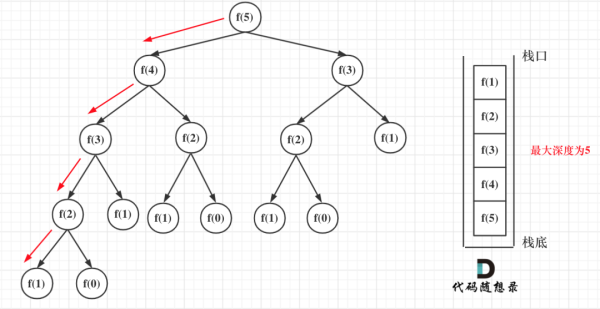
遞歸第n個斐波那契數的話,遞歸調用棧的深度就是n。
那么每次遞歸的空間復雜度是O(1), 調用棧深度為n,所以這段遞歸代碼的空間復雜度就是O(n)。
int fibonacci(int i) { if(i <= 0) return 0; if(i == 1) return 1; return fibonacci(i-1) + fibonacci(i-2); }最后對各種求斐波那契數列方法的性能做一下分析,如題:
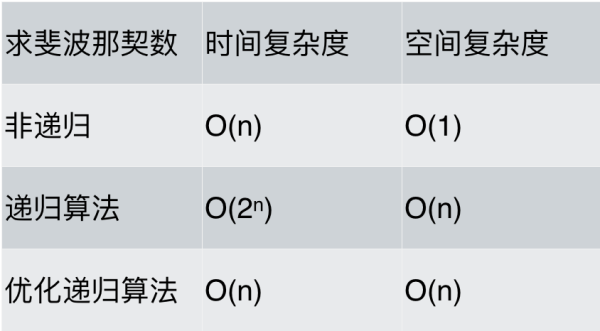
可以看出,求斐波那契數的時候,使用遞歸算法并不一定是在性能上是最優的,但遞歸確實簡化的代碼層面的復雜度。
帶大家再分析一段二分查找的遞歸實現。
int binary_search( int arr[], int l, int r, int x) { if (r >= l) { int mid = l + (r - l) / 2; if (arr[mid] == x) return mid; if (arr[mid] > x) return binary_search(arr, l, mid - 1, x); return binary_search(arr, mid + 1, r, x); } return -1; }都知道二分查找的時間復雜度是O(logn),那么遞歸二分查找的空間復雜度是多少呢?
我們依然看 每次遞歸的空間復雜度和遞歸的深度
首先我們先明確這里的空間復雜度里面的n是什么?二分查找的時候n就是指查找數組的長度,也就是代碼中的arr數組。
每次遞歸的空間復雜度可以看出主要就是參數里傳入的這個arr數組,即:O(n)。
再來看遞歸的深度,二分查找的遞歸深度是logn ,遞歸深度就是調用棧的長度,那么這段代碼的空間復雜度為 n * logn = O(nlogn)。
其實還是因為這個數組,我們可以把這個數組放到外面而不是放在遞歸函數參數里里,代碼如下:
int arr[] = {2, 3, 4, 5, 8, 10, 15, 17, 20}; int binary_search(int l, int r, int n) { if (r >= l) { int mid = l + (r - l) / 2; if (arr[mid] == n) return mid; if (arr[mid] > n) return binary_search(l, mid - 1, n); return binary_search(mid + 1, r, n); } return -1; }看這份代碼將arr數組定義為全局變量,而不放在遞歸循環里,那么每層遞歸的空間復雜度是O(1),遞歸深度為O(logn),整體空間復雜度為 1 * logn = O(logn)。
到此,關于“什么是遞歸算法”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。