如何理解動態數組和時間復雜度

本篇內容主要講解“如何理解動態數組和時間復雜度”，感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷，實用性強。下面就讓小編來帶大家學習“如何理解動態數組和時間復雜度”吧!

一、數組基礎

1.1 定義

數組(Array)是一種線性表數據結構，它用一組連續的內存空間來存儲一組具有相同類型的數據。

1.2 創建流程

當我們在 java 中當創建一個數組時，會在內存中劃分出一塊 連續的內存，當有數據進入的時候會將數據  按順序的存儲在這塊連續的內存中。當需要讀取數組中的數據時，需要提供數組中的 索引，然后數組根據索引將內存中的數據取出來，返回給讀取程序。

把數據碼成一排進行存放：

所有的數據結構都支持幾個基本操作：讀取、插入、刪除數組索引可以有語意，也可以沒有語意，比如說  student[2]，就代表是這個數組中的第三個學生。

因為數組在存儲數據時是按順序存儲的，存儲數據的內存也是連續的，所以數組最大的優點就是能夠  快速查詢，尋址讀取數據比較容易，但是插入和刪除就比較困難。

為什么數組最大的優點就是能夠 快速查詢。因為當我們在讀取數據時，只需要告訴數組獲取數據的索引位置就可以了，數組就會把對應位置的數據，讀取出來

插入和 刪除比較困難是因為這些存儲數據的內存是連續的，數組大小固定，插入和刪除都需要移動元素

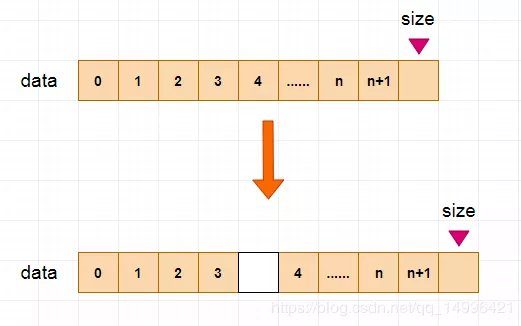
例如：一個數組中編號  0>1>2>3>4這五個內存地址中都存了數組的數據，但現在你需要往4中插入一個數據，那就代表著從4開始，后面的所有內存中的數據都要往后移一個位置。

二、編寫我們自己的數組類

我們知道想要維護某一個數據，我們需要對這個數據有這最基本的  增、刪、改、查，這幾個基本功能，所以我們自己手動編寫的數組類，也是需要有用這幾個最基本的功能，雖然不會像  List、Map這些類，那么強大，但是對于我們普通的開發來說，基本是可以滿足，下圖所示就是我們一個基本的數組類，那么我們是如何對數組進行改造，來編寫一個屬于我們自己的數組類的呢，這里我們以  增加和刪除做重點講解，本文中的所有源碼會在最后貼出來，請往下看。

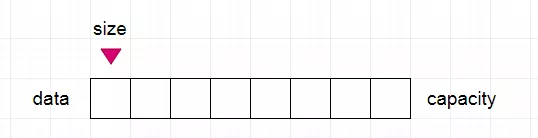
從上圖中我們可以得知，我們創建數組類的時候，需要三個元素 data、size、capacity，而我們所需要使用的數組，肯定是要能夠支持  多種數據類型，而不是單一的數據結構，因此，我們可以在設計類的時候，是需要加上泛型支持，讓我們的數據結構可以支持放置 任何數據類型。

data：需要傳遞的數據size：元素中的個數capacity：數組的初始容量

注意：我們上面所說的放置  任何數據類型，只能是類對象，不可以是基本數據類型，但是我們每個基本數據類型都有對應的包裝類，所以我們的基本類型也是可以使用的，不過只是使用的是它的包裝類

因此，我們在設計我們的數組類的時候，我們可以這么設計

/**  * @program:   * @ClassName ArrayPlus  * @description:  * @author: lyy  * @create: 2019-11-18 22:27  * @Version 1.0  **/ public class ArrayPlus<E> {      private E[] data;     private int size;      //構造函數，傳入數組的容量capacity 構造array     public ArrayPlus(int capacity){         data = (E[])new Object[capacity];         size = 0;     }     //無參數的構造函數，傳入數組的容量capacity=10     public ArrayPlus(){         this(10);     }      //獲取元素中的個數     public int getSize(){         return size;     }      //獲取數組的容量     public int getCapacity(){         return data.length;     }      //返回數組是否為空     public boolean isEmpty(){         return size == 0;     }      @Override     public String toString(){         StringBuffer res = new StringBuffer();         res.append(String.format("Array：Size = %d，capacity = %d\n",size,data.length));         res.append("[");         for (int i = 0; i < size; i++) {             res.append(data[i]);             if(i != size - 1)                 res.append("，");         }         res.append("]");         return res.toString();     }  }

2.1 數組添加元素

在數組中是如何添加數據的呢，首先我們需要創建一個 擁有初始容量的數組，當我們創建完成之后，size是指向第一個元素的，也就是  index=0的地方，當我們添加第一個數據后 也就是 data[0]=12后，我們的元素中的個數 size，需要往后挪一位的，也就是  size++的操作，每當我們操作一位，就需要將上面的操作重復執行，直到最后一個元素添加到我們的數組中。

如下圖所示：

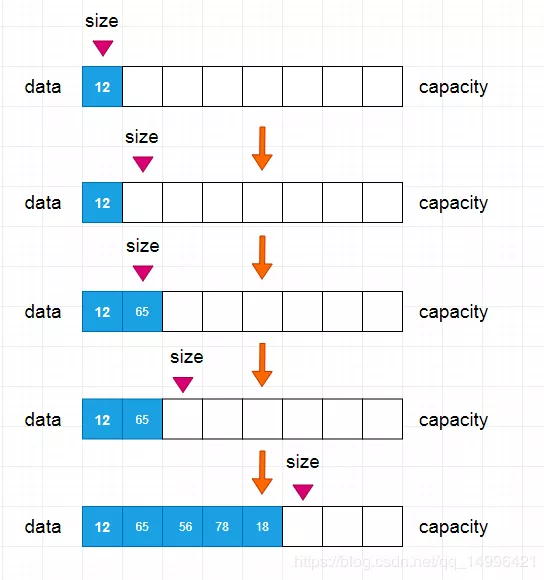
知道了怎么操作，但是我們要如果通過代碼來完成呢?

首先我們要清楚在添加的時候， 在哪里?添加什么數據?，在哪里：我們要在數據的什么地方進行添加，也就是要添加到數組中的哪個下標——  index的地方，知道了在下標，我們只需要將添加的數據，添加到數組中為 index  的地方即可，除此之外，我們只需要對添加時，做一些基本的判斷就可以了，代碼如下：

//在所有元素后添加一個新元素   public void addLast(E e){       add(size,e);   }    //想所有元素前添加一個新元素   public void addFirst(E e){       add(0,e);   }    //在第Index個位置插入一個新元素e   public void add(int index,E e){       if(size == data.length)           throw new IllegalArgumentException("Add failed . Array is full.");        if(index < 0 || index > size)           throw new IllegalArgumentException("Add failed . Require index < 0 || index > size.");        for (int i = size - 1; i >= index ; i--)           data[i+1] = data[i];        data[index]  = e;       size++;   }

測試代碼：

public class Main2 {      public static void main(String[] args) {         ArrayPlus<Integer> arr = new ArrayPlus<>();         for (int i = 12; i < 16; i++)             arr.addLast(i);         System.out.println(arr);     } }

返回結果：

Array：Size = 4，capacity = 10 [12，13，14，15]

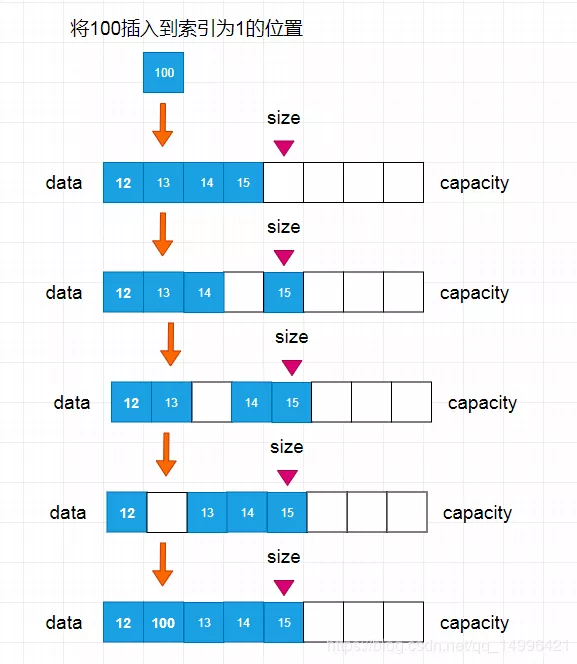
在數組中是如何執行插入呢?如下圖所示：

測試代碼：

public static void main(String[] args) {         ArrayPlus<Integer> arr = new ArrayPlus<>();        for (int i = 12; i < 16; i++)            arr.addLast(i);        System.out.println(arr);         arr.add(1,100);        System.out.println(arr);      }

返回結果：

Array：Size = 4，capacity = 10 [12，13，14，15] Array：Size = 5，capacity = 10 [12，100，13，14，15]

2.2 數組刪除元素

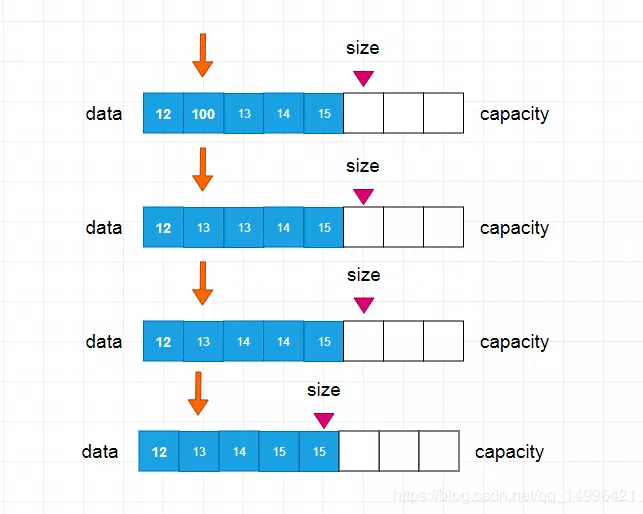
如果我們想要刪除 索引為1的元素，是怎樣操作的呢，首先我們需要先將 索引為2的數據，覆蓋到 索引為1的元素上，再將 索引為3的數據放到  索引為2上，依次循環操作，直到最后一位元素，我們在將最后一位元素的數據設置為  null，這樣垃圾回收機制就會自動幫我們清除這個元素。整個過程就完成了刪除元素的功能，具體流程如下圖所示：

實現代碼：

//查找數組中元素e所在的索引，如果不存在元素e，則返回-1     public int find(E e){         for (int i = 0; i < size; i++) {             if(data[i].equals(e))                 return i;         }         return -1;     }   //從數組中刪除index位置的元素，返回刪除的元素     public E remove(int index){         if(index < 0 || index >= size)             throw new IllegalArgumentException("remove failed . Index is illegal.");          E ret = data[index];         for (int i = index+1 ; i < size; i++)                 data[i - 1] = data[i];          size--;         // loitering objects != memory leak         data[size] = null;//如果一旦使用新的元素，添加新的對象就會覆蓋掉         return ret;     }      //從數組中刪除第一個位置的元素，返回刪除的元素     public E removeFirst(){         return remove(0);     }      //從數組中刪除最后一個位置的元素，返回刪除的元素     public E removeLast(){         return remove(size-1);     }      //從數組中刪除元素e     public void removeElement(E e){         int index = find(e);         if(index != -1)             remove(index);      }

測試：

import com.bj.array.ArrayPlus;  public class Main2 {      public static void main(String[] args) {          ArrayPlus<Integer> arr = new ArrayPlus<>();         for (int i = 12; i < 16; i++)             arr.addLast(i);         System.out.println(arr);          arr.add(1,100);         System.out.println(arr);          arr.remove(1);         System.out.println(arr);       }  }

返回示例：

Array：Size = 4，capacity = 10 [12，13，14，15] Array：Size = 5，capacity = 10 [12，100，13，14，15] Array：Size = 4，capacity = 10 [12，13，14，15]

我們看到結果已經把索引為1的刪除了，到這里我們已經完成了一大半了，還有一小點也是最重要的，就是當我們添加數據超過了我們的初始容量大小的時候，就會報錯，初始容量，無法添加超過的數據，那么我們應該怎么操作呢?其實很簡單，我們只需要給我們數組類，添加一個擴容的方法即可，當我們元素的個數等于數組長度的時候，我們就進行擴容，我們稱之為  動態數組。

2.3 動態數組

前邊我們講過的用new給基本類型和對象在運行時分配內存，但它們的已經在編譯時就已經確定下來，因為我們為之申請內存的數據類型在程序里有明確的定義，有明確的單位長度。但是，總有些時候，必須要等到程序運行時才能確定需要申請多少內存，甚至還需要根據程序的運行情況追加申請更多的內存。從某種意義上講，這樣的內存管理才是真正的動態。下面，我將帶大家編寫一個程序為一個整數型數組分配內存，實現動態數組。當你們看到下面這個圖的時候，有沒有想到什么，沒錯，有點像C++里面的指針

實現代碼：

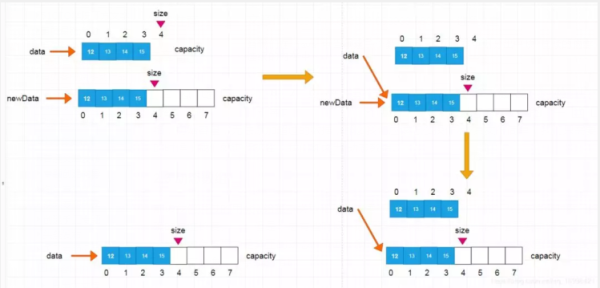
//在第Index個位置插入一個新元素e    public void add(int index,E e){         if(index < 0 || index > size)            throw new IllegalArgumentException("Add failed . Require index < 0 || index > size.");         if(size == data.length)            resize(2 * data.length);          for (int i = size - 1; i >= index ; i--)            data[i+1] = data[i];         data[index]  = e;        size++;    }     private void resize(int newCapacity) {        E[] newData = (E[])new Object[newCapacity];        for (int i = 0; i < size; i++)            newData[i] = data[i];        data = newData;    }

動態數組測試：

import com.bj.array.ArrayPlus;  public class Main2 {      public static void main(String[] args) {         ArrayPlus<Integer> arr = new ArrayPlus<>();         for (int i = 0; i < 10; i++)             arr.addLast(i);         System.out.println(arr);          arr.add(1,100);         System.out.println(arr);          for (int i = 0; i < 6; i++)             arr.remove(i);          arr.removeLast();         System.out.println(arr);     } }

測試結果：

Array：Size = 10，capacity = 10 [0，1，2，3，4，5，6，7，8，9] Array：Size = 11，capacity = 20 [0，100，1，2，3，4，5，6，7，8，9] Array：Size = 4，capacity = 10 [100，2，4，6]

從結果中我們可以看到，當我們數組元素超過初始容量大小時，自動擴容到初始容量的  兩倍也就是20，當我們數組長度小于1/4的時候，為什么是1/4的時候而不是1/2的時候呢，下面我們會做詳細介紹。當我們數組長度小于1/4的時候，會自動縮回到初始10的容量，不會去占據大量的內存空間。

三、時間復雜度分析

3.1 基礎

五種常見的時間復雜度 1) O(1)：常數復雜度, 最快的算法，數組的存取是O(1) 1) O(n)：線性復雜度, 例如：數組,  以遍歷的方式在其中查找元素 1) O(logN)：對數復雜度 1) O(nlogn)：求兩個數組的交集,  其中一個是有序數組，A數組每一個元素都要在B數組中進行查找操作，每次查找如果使用二分法則復雜度是 logN 1)  O(n2)：平方復雜度，求兩個無序數組的交集

在這里，大O描述的是算法的運行時間和輸入數據之間的關系

3.2 舉例說明

大家可以看下面一個例子

public static int sum(int[] nums){   int sum = 0;   for(int num: nums) sum += num;   return sum; }

• 這個算法是 O(n) 復雜度的，其中 n是nums中的元素個數，算法和n呈線性關系

• 為什么說他是 O(n)的時間復雜度呢，因為這個算法運行的時間的多少是和 nums中元素的個數成線性關系的，那么這個線性關系，表現在我們的 n  是一次方，它不是 O(n) 方的，也不是 O(n) 的立方，n 對應的是一次方。

• 我們忽略常數，實際時間是：T=c1*n+c2c1：我們要把這個數據從 nums數組中取出來，其次我們還要把 sum這個數取出來，然后 num這個數和  sum相加，最終呢我們要這個結果扔回給 sum中c2：開始開辟了一個Int型的空間，我們把它叫 sum ，要把 0 初始化賦值給sum，在最終呢我們還要把這個  sum 給 return 回去

一方面把 c1 和 c2 具體分析出來是不大必要的，另一方面也是不太可能的，為什么說不可能呢?如果說把 num 從 nums 中取出來，基于  不同的語言，基于 不同的實現，它實際運行的 時間是不等的，就算轉換成機器碼，它對應的機器碼的指令數也有可能是不同的，就算是指令數是相同的，同樣的一個指令，在我們  cpu 的底層，你使用的 cpu 不同，很有可能，執行的操作也是不同的，所以在實際上我們可能說出 c1 是幾條指令，但是卻很難說出 c1  到底是多少，c2也是同理，正因為如此，我們在進行時間復雜度時，是忽略這些常數的。

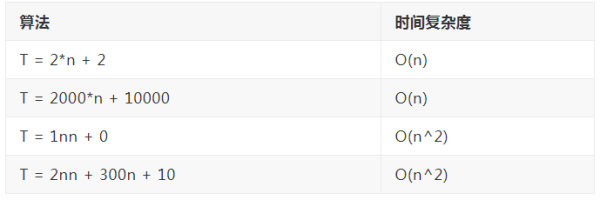
忽略這些常數就意味著什么，就意味著這些 t=2*n+2和t=2000*n+10000算法這些都是 O(n)  的算法，見下面列表：換句話說他們都是線性數據的算法，也就是說我們這個算法消耗的時間是和我們輸入數據的規模成一個線性相關的，  t=1*n*n+0也線性算法是和我們成平方關系的 ，他的性能比上面的差，因為他是 O(n^2)的

O(n)和O(n^2)并不代表說 O(n)的算法快于 O(n^2)的算法，我們要看 n 的常數，比如 n=3000的時候，或者 n>3000的時候，  O(n^2)消耗的時間是遠遠大于 O(n)的，n越大 O(n)遠遠快于  O(n^2)O：描述的是一個算法，也就是說漸進時間復雜度當高階項和低階項同時出現的時候，低階項會被忽略，比如說：T=2*n*n+300n+10當中  2*n*n，是 O(n^2)級別的算法，屬于高階項， 300n是 O(n)的算法低階項，當n無窮大的時候，低階項起的作用很小。

3.3 分析動態數組的時間復雜度

3.3.1 添加操作

添加操作 總體來說屬于 O(n) 級別的復雜度，如下列表

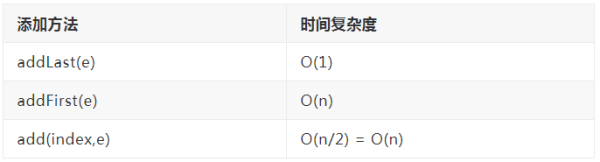
在程序設計中，我們要采用最嚴謹的設計，需要考慮到最壞的情況，所以我們說添加操作時屬于 O(n)級別的復雜度，是因為我們在  addLast的時候，有可能會進行 resize的操作，我們從最壞的情況分析是對的，但是 addLast不可能每次都是進行 resize操作，比如 size  有十個，我們要添加十個元素后才會觸發一個 resize,我們要在添加十個元素才會觸發一個 resize，因此我們使用最壞情況進行分析的是不合理的，那么分析  addLast時間復雜度呢，請看下面小節。

3.3.2 resize的復雜度分析

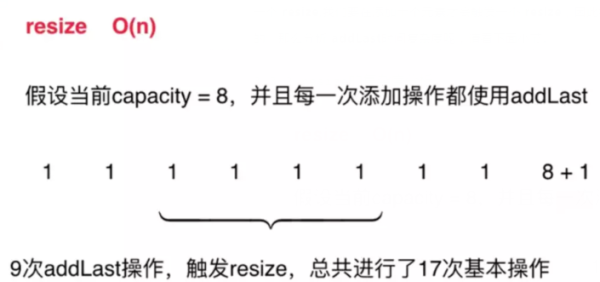
總共進行了17次基本操作：9次添加操作8次元素轉移操作

• 9次addLast操作，觸發resize，總共進行了17次基本操作，平均每次addLast操作，進行了2次基本操作

• 假設 capacity = n，n+1  次addLast，觸發resize，總共進行了2n+1次基本操作，平均，每次addLast操作，進行了2次基本操作

• 這樣均攤計算，時間復雜度是O(1)的，在這個例子里，這樣均攤計算，比計算最壞情況有意義

• addLast 均攤復雜度是O(1)的，同理我們看 removeLast操作，均攤復雜度也是O(1)

3.3.3 復雜度震蕩

當我們數組容量滿了的時候，因為是動態數組，回去自動擴容，我們又馬上去remove 一個操作的時候，因為數組容量小于 初始容量的一半的時候，又會 自動  resize縮減為一半的大小，如此操作，就會一個問題，就是我們在 removeLast的時候 resize 過于著急(Eager)

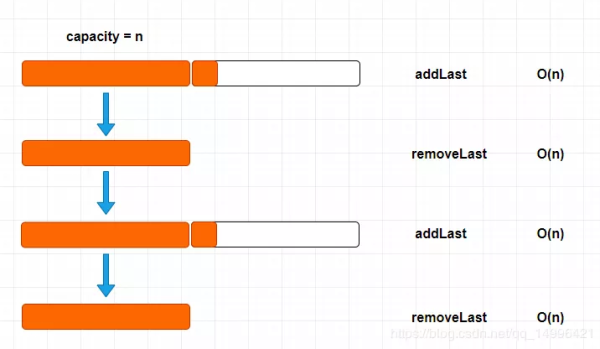
解決方案：Lazy，懶散的，其實也很簡單，如下圖所示：

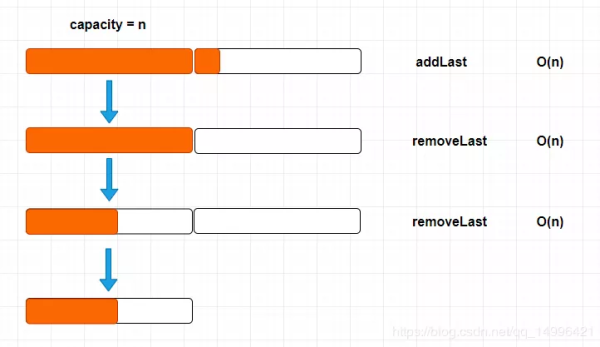
當我們的 size == capacity /4 時候，才將capacity 減半，實現方式如下：

//從數組中刪除index位置的元素，返回刪除的元素     public E remove(int index){         if(index < 0 || index >= size)             throw new IllegalArgumentException("remove failed . Index is illegal.");          E ret = data[index];         for (int i = index+1 ; i < size; i++)                 data[i - 1] = data[i];          size--;         // loitering objects != memory leak         data[size] = null;//如果一旦使用新的元素，添加新的對象就會覆蓋掉          if(size == data.length / 4 && data.length / 2 != 0)             resize(data.length / 2);          return ret;     }

完整代碼：

package com.bj.array;   /**  * @program: Data-Structures  * @ClassName Array  * @description:  * @author: lyy  * @create: 2019-11-18 22:27  * @Version 1.0  **/ public class ArrayPlus<E> {      private E[] data;     private int size;      //構造函數，傳入數組的容量capacity 構造array     public ArrayPlus(int capacity){         data = (E[])new Object[capacity];         size = 0;     }     //無參數的構造函數，傳入數組的容量capacity=10     public ArrayPlus(){         this(10);     }      //獲取元素中的個數     public int getSize(){         return size;     }      //獲取數組的容量     public int getCapacity(){         return data.length;     }      //返回數組是否為空     public boolean isEmpty(){         return size == 0;     }      //在所有元素后添加一個新元素     public void addLast(E e){         add(size,e);     }      //想所有元素前添加一個新元素     public void addFirst(E e){         add(0,e);     }      //在第Index個位置插入一個新元素e     public void add(int index,E e){          if(index < 0 || index > size)             throw new IllegalArgumentException("Add failed . Require index < 0 || index > size.");          if(size == data.length)             resize(2 * data.length);           for (int i = size - 1; i >= index ; i--)             data[i+1] = data[i];          data[index]  = e;         size++;     }        //獲取index索引位置的元素    public E get(int index){         if(index < 0 || index >= size)             throw new IllegalArgumentException("Get failed . Index is illegal.");          return data[index];     }      //修改index索引位置的元素為e     public void set(int index,E e){         if(index < 0 || index >= size)             throw new IllegalArgumentException("Set failed . Index is illegal.");           data[index] = e;     }      //查找數組中是否有元素e     public boolean contains(E e){         for (int i = 0; i < size; i++) {             if(data[i].equals(e))                 return true;         }         return false;     }      //查找數組中元素e所在的索引，如果不存在元素e，則返回-1     public int find(E e){         for (int i = 0; i < size; i++) {             if(data[i].equals(e))                 return i;         }         return -1;     }      //從數組中刪除index位置的元素，返回刪除的元素     public E remove(int index){         if(index < 0 || index >= size)             throw new IllegalArgumentException("remove failed . Index is illegal.");          E ret = data[index];         for (int i = index+1 ; i < size; i++)                 data[i - 1] = data[i];          size--;         // loitering objects != memory leak         data[size] = null;//如果一旦使用新的元素，添加新的對象就會覆蓋掉          if(size == data.length / 4 && data.length / 2 != 0)             resize(data.length / 2);          return ret;     }      //從數組中刪除第一個位置的元素，返回刪除的元素     public E removeFirst(){         return remove(0);     }      //從數組中刪除最后一個位置的元素，返回刪除的元素     public E removeLast(){         return remove(size-1);     }      //從數組中刪除元素e     //思考？如果返回是否刪除成功 2、如果存在重復數據，如何刪除多個     public void removeElement(E e){         int index = find(e);         if(index != -1)             remove(index);      }      @Override     public String toString(){         StringBuffer res = new StringBuffer();         res.append(String.format("Array：Size = %d，capacity = %d\n",size,data.length));         res.append("[");         for (int i = 0; i < size; i++) {             res.append(data[i]);             if(i != size - 1)                 res.append("，");         }         res.append("]");         return res.toString();     }      private void resize(int newCapacity) {         E[] newData = (E[])new Object[newCapacity];         for (int i = 0; i < size; i++)             newData[i] = data[i];         data = newData;     }  }

到此，相信大家對“如何理解動態數組和時間復雜度”有了更深的了解，不妨來實際操作一番吧！這里是億速云網站，更多相關內容可以進入相關頻道進行查詢，關注我們，繼續學習！