DAG上DP的示例分析

這篇文章給大家分享的是有關DAG上DP的示例分析的內容。小編覺得挺實用的，因此分享給大家做個參考，一起跟隨小編過來看看吧。

DAG即有向無環圖

這里舉出兩經典的DAG模型，嵌套矩形和硬幣問題

嵌套矩形(不固定起點最長路及其字典序)

描述

有n個矩形，每個矩形可以用 (a,b) 來描述，表示長和寬
矩形 X(a,b) 可以嵌套在矩形 Y(c,d) 中，當且僅當 a<c,b<d 或者 b<c,a<d(旋轉90度)
例如(1,5)可以嵌套在(6,2)內，但不能嵌套在(3,4)中
你的任務是選出盡可能多的矩形排成一行，使得除最后一個外，每一個矩形都可以嵌套在下一個矩形內

分析

矩形間的“可嵌套”關系是一個典型的二元關系，二元關系可以用圖來建模
如果矩形X可以嵌套在Y中，則就從X到Y連一條有向邊
這個圖是無環的，因為一個矩形無法直接或或間接的嵌套在自己的內部
也即是說這是以一個DAG
因此，我們就是在求DAG上的不固定起點的最長路徑

解題

設 d(i) 表示從結點 i 出發的最長路長度

第一步只能走到它的相鄰點，那么我們就有：

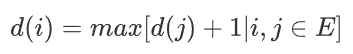
其中，E為邊集，則最終答案是所有的d(i)中的最大值，因此可以用遞推或者記憶化搜索計算

第一步，建圖，假如用鄰接矩陣將矩形間的關系保存在矩陣G中

第二步，編寫記憶化搜索程序(調用前先初始化數組為0)

第三步，按字典序輸出最佳的方案

假如有這樣的 5 個矩形，輸入的邊長分別是：

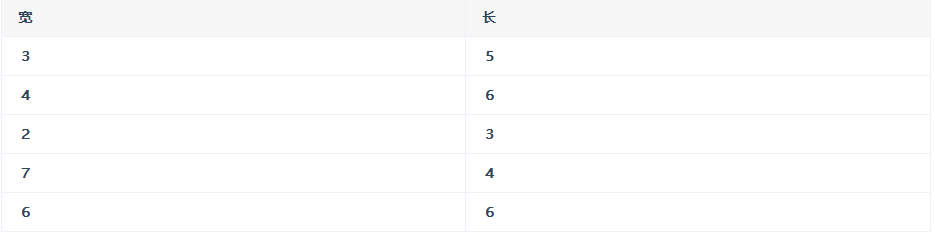
建圖

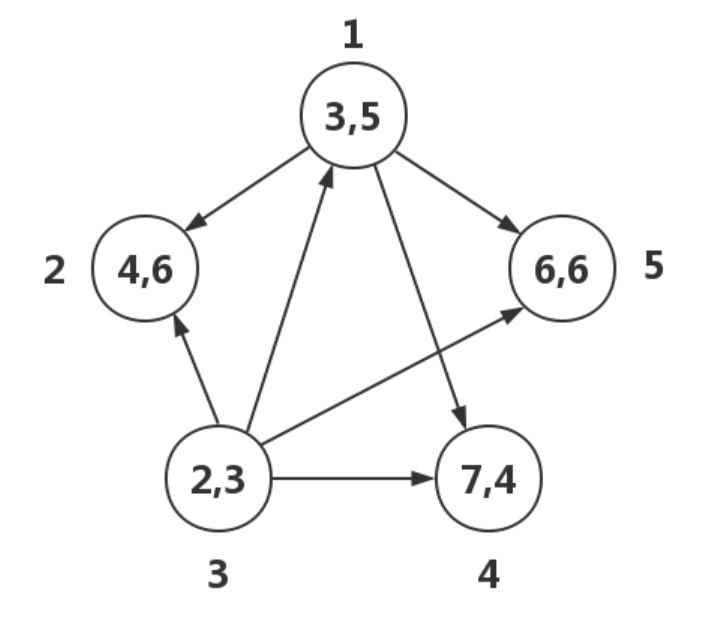
先對長和寬來此排序，再按照要求構圖， 完成之后，直接記憶化搜索，但由于是不固定起點的，所以不能只從第一個點搜索，而是每個點都要開始搜索

搜索代碼：

int dp(int i)
{
    int& ans = d[i];//為表項d[i]聲明一個引用ans 
    if(ans > 0)  
        return ans;
    ans = 1;
    for(int j=1;j<n;j++)
        if(G[i][j])
			ans = max(ans,dp(j)+1);
    return ans;
}

這里使用了一個技巧：為表項d[i]聲明一個引用ans，這樣，任何對ans的讀寫實際上都是在對d[i]進行。當d[i]換成d [i] [j] [k] [l] [m] [n] 這樣很長的名字時，該技巧的優勢就會很明顯

然后我們要考慮如何輸出字典序最小的方案
字典序只是消除并列名次的方法，我們最根本的任務還是求出最長路
在把所有的d值計算出來后，選擇最大的d[i]所對應的i，而如果有多個i，則選擇最小的i，來保證字典序最小
接下來選擇 d(i) = d(j) +1 且i, j ∈E 的任何一個j，但是為滿足字典序最小，需選擇最小的j，代碼如下

void print_ans(int i){
    printf("%d ", i);//第一次i代表最長路的起點節點，以后均代表從該節點開始的路徑
    for(int j = 1; j <= n; j++)
        if(G[i][j] && d[i] == d[j]+1)// 如果該圖滿足可嵌套，且d[i] = d[j] +1
        {
            print_ans(j);
            //立即輸出從節點j開始的路徑
            break;
        }
}

完整題解代碼

#include<stdio.h>
#include<string.h>
#define MAXN 100+1
int n, G[MAXN][MAXN];//存圖
int x[MAXN], y[MAXN], d[MAXN]; 

int dp(int i){
    int& ans = d[i];//為表項d[i]聲明一個引用ans 
    if(ans > 0)  
        return ans;
    ans = 1;
    for(int j=1;j<=n;j++)
        if(G[i][j])
			ans = max(ans,dp(j)+1);
    return ans;
}

void print_ans(int i){
    printf("%d ", i);//第一次i代表最長路的起點節點，以后均代表從該節點開始的路徑
    for(int j = 1; j <= n; j++)
        if(G[i][j] && d[i] == d[j]+1)// 如果該圖滿足可嵌套，且d[i] = d[j] +1
        {
            print_ans(j);
            //立即輸出從節點j開始的路徑
            break;
        }
}

int main()
{
    int t, ans, best;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        scanf("%d%d", &x[i], &y[i]);
        if(x[i] > y[i]){
            t = x[i];
            x[i] = y[i];
            y[i] = t;   
            //保證X[]存的是長，Y[]存的是寬
        }
    }
    memset(G, 0, sizeof(G));
    for(int i = 1; i <= n; i++)//建圖
        for(int j = 1; j <= n; j++)
            if(x[i] < x[j] && y[i] < y[j])
                G[i][j] = 1;//如果第i個矩形的長寬均小于第j個，使圖相應的值為1

    ans = 0;
    for(int i = 1; i <= n; i++)//依次遞推所有的的節點
        if(dp(i) > ans){
            best = i;//best是最小字典序
            ans = dp(i);
        }
    printf("ans=%d\n", ans);//表示最長路長度
    print_ans(best);
    printf("\n");
    return 0 ;
}

硬幣問題(固定終點的最長路和最短路)

描述

有 n 種硬幣，面值分別為V1, V2······Vn，每種都有無限多
給定非負整數 S ，可以選用多少個硬幣，使得面值之和恰好為S？
輸出硬幣數目的最小值和最大值

分析

看上去和嵌套矩形問題很不一樣，但本題的本質也是DAG上的路徑問題
將每種面值看作一個節點，設初始狀態為S，目標狀態為0
若當前在狀態 i，每使用一個硬幣 j，狀態便轉移到i - Vj

解題

最長路和最短路的求法是類似的，由于終點固定，d(i) 的確切含義變為從結點i出發到結點0的最長路徑長度

int dp(int S)
{
    int& ans = d[S];
    if(ans >= 0) 
        return ans;
    ans = 0;
    for(int i=1;i<=n;i++)
        if(S >= V[i])    
            ans = max(ans,dp(S-V[i])+1);
    return ans;
}

回顧一下嵌套矩形的找最長路

int dp(int i)
{
    int& ans = d[i];//為表項d[i]聲明一個引用ans 
    if(ans > 0)
        return ans;
    ans = 1;
    for(int j=1;j<n;j++)
        if(G[i][j])
			ans = max(ans,dp(j)+1);
    return ans;
}

由于在本題中，路徑長度是可以為0的(S本身可以是0)，所以不能再用d=0表示這個d值還沒有算過，初始化時也不能再把d全設為0，而要設置為一個負值令初始狀態不合法，這里可以用 -1 來表示沒有算過，初始化時只需用memset(d,-1,sizeof(d))即可，同時 if(ans>0) 也要改成 if(ans>=0)

但其實，由于結點S不一定真的能到達結點0，所以需要用特殊的d[S]值表示“無法到達”，但在上述代碼中，如果S根本無法繼續往前走，返回值是0，將被誤以為是“已到達終點”的意思

如果把ans初始化為-1呢？但-1代表“還沒算過”，所以返回-1相當于放棄了自己的勞動成果

如果把ans初始化為一個很大的整數，從目前來看，它也會被認為是“還沒算過”，但至少可以和所有d的初值分開——只需把代碼中if(ans>=0)改為if(ans!=-1)即可

int dp(int S)
{
    int& ans = d[S];
    if(ans != -1)   
        return ans;
    ans = -(1<<30);
    for(int i=1;i<=n;i++){
        if(S >= V[i])    
            ans = max(ans,dp(S-V[i])+1);
    }
    return ans;
}

另一個常用的解決方法是不用特殊值表示“還沒算過”，而用另外一個數組 vis[i] 表示狀態 i 是否被訪問過

int dp(int S)
{
    if(vis[S])  
        return d[S];
    vis[S] = -1;
    int& ans = d[S];
    ans = -(1<<30);
    for(int i=1;i<=n;i++)
        if(S >= V[i])    
            ans = max(ans,dp(S-V[i])+1);
    return ans;
}

本題要求最小、最大兩個值，記憶化搜索就必須寫兩個，在這種情況下，用遞推更加方便(此時需注意遞推的順序)

minv[0] = maxv[0] = 0;
for(int i=1;i<=S;i++){
    minv[i] = INF;//minv[i]表示最小值
    maxv[i] = -INF;//maxv[i]表示最大值
}
for(int i=1;i<=S;i++){
    for(int j=1;j<=n;j++){
        if(i >= V[j]){
            minv[i] = min(minv[i],minv[i-V[j]]+1);
            maxv[i] = max(maxv[i],maxv[i-V[j]]+1);
        }
    }
}
printf("%d %d\n",minv[S],maxv[S]);

如何輸出字典序最小的方案呢？剛剛介紹的方法仍然適用，如下所示：

void print_ans(int* d,int S)
{
    for(int i=1; i<=n; i++)
    {
        if(S>=V[i] && d[S]==d[S-V[i]]+1)
        {
            printf("%d ",i);
            print_ans(d,S-V[i]);
            break;

        }
    }
}

上題打印的是路徑上的點，而這里打印的是路徑上的邊

另外一種常用的打印路徑的方法：遞推時直接用min_coin[S]記錄滿足min[S]==min[S-V[i]]+1的最小的i，則打印路徑時可以省去print_ans()中的循環，并可以方便地把遞歸改成迭代 (當然，原來的也可以改成迭代，但不那么自然）具體代碼如下

for(int i=1;i<=S;i++){
    for(int j=1;j<=n;j++){
        if(i >= V[j]){
            if(min[i]>min[i-V[j]]+1){
                min[i] = min[i-V[j]]+1;
                min_coin[i] = j;
            }
            if(max[i]<max[i-V[j]]+1){
                max[i] = max[i-V[j]]+1;
                max_coin[i] = j;
            }
        }
    }
}

小結

由于DAG最長 (短）路的特殊性，有兩種“對稱”的狀態定義方式。

狀態1：設 d(i) 為從 i 出發的最長路，則

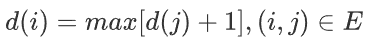
狀態2：設 d(i) 為以 i 結束的最長路，則

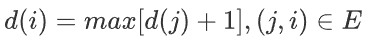
如果使用狀態2，“硬幣問題”就變得和“嵌套矩形問題”幾乎一樣了 (唯一的區別是“嵌套矩形問題”還需要取所有d (i）的最大值）！我們在上面介紹了比較麻煩的狀態1，主要是為了展示一些常見技巧和陷阱，實際比賽中不推薦使用。

使用狀態2時，有時還會遇到一個問題：狀態轉移方程可能不好計算，因為在很多時候，可以方便地枚舉從某個結點i出發的所有邊 (i , j），卻不方便“反著”枚舉 (j , i）。特別是在有些題目中，這些邊具有明顯的實際背景，對應的過程不可逆。這時需要用“刷表法”

什么是“刷表法”呢？傳統的遞推法可以表示成“對于每個狀態 i，計算f (i）”，或者稱為“填表法”。這需要對于每個狀態 i，找到f (i）依賴的所有狀態，在某些情況下并不方便。另一種方法是“對于每個狀態i，更新f (i）所影響到的狀態”，或者稱為“刷表法”。對應到DAG最長路的問題中，就相當于按照拓撲序枚舉 i，對于每個 i，枚舉邊 (i , j），然后更新d[j] = max(d[j],d[i]+1)。注意，一般不把這個式子叫做“狀態轉移方程”，因為它不是一個可以直接計算d[j]的方程，而只是一個更新公式

提示：傳統的遞推法可以表示成“對于每個狀態 i，計算f (i）”，或者稱為“填表法”。這需要對于每個狀態 i，找到f (i）依賴的所有狀態，在某些時候并不方便。另一種方法是“對于每個狀態 i，更新f (i）所影響到的狀態”，或者稱為“刷表法”，有時比填表法方便。但需要注意的是，只有當每個狀態所依賴的狀態對它的影響相互獨立時才能用刷表法

例題

A - A Spy in the Metro

某城市的地鐵是線性的，有n（2≤n≤50）個車站，從左到右編號為1～n

有M1輛列車從第1站開始往右開，還有M2輛列車從第n站開始往左開

在時刻0，Mario從第1站出發，目的是在時刻T（0≤T≤200）會見車站n的一個間諜，在車站等車時容易被抓，所以她決定盡量躲在開動的火車上，讓在車站等待的總時間盡量短，列車靠站停車時間忽略不計，且Mario身手敏捷，即使兩輛方向不同的列車在同一時間靠站，Mario也能完成換乘。

輸入：

第1行為n，
第2行為T，
第3行有n－1個整數t1,t2,…,tn?1（1≤ti≤70），
其中ti表示地鐵從車站i到i＋1的行駛時間（兩個方向一樣）
第4行為M1（1≤M1≤50），即從第1站出發向右開的列車數目
第5行包含M1個整數d1, d2,…, dM1（0≤di≤250，di＜di+1），即各列車的出發時間。
第6、7行描述從第n站出發向左開的列車，格式同第4、5行

輸出僅包含一行，即最少等待時間。無解輸出impossible

分析

時間是單向流逝的，是一個天然的“序”，而影響到決策的只有當前時間和所處的車站
可以用 d(i,j) 表示：在時刻i，處于在車站j（編號為1～n）時，最少還需要等待的時間
邊界條件是d(T,n)=0，其他 d(T,i)（i不等于n）為正無窮

有如下3種決策。

• 等1分鐘。

• 搭乘往右開的車（如果有）

• 搭乘往左開的車（如果有）

在程序中定義一個三維數組has_train
has_train [t] [i] [0] 表示：時刻t，在車站i是否有往右開的火車
has_train [t] [i] [1] 表示：時刻t，在車站i是否有往左開的火車

核心代碼如下：

for (int i = 1; i <= n-1; i++)
    dp[T][i] = INF;
dp[T][n] = 0;

for (int i = T-1; i >= 0; i++)
{
    for (int j = 1; j <=n ; j++)
    {
        dp[i][j] = dp[i+1][j] + 1;
        if(j<n && has_train[i][j][0] && i+t[j] <= T)
            dp[i][j] = min(dp[i][j],dp[i+t[j][j+1]])//右
        if(j>1 && has_train[i][j][1] && i+t[j-1] <= T)
            dp[i][j] = min(dp[i][j],dp[i+t[j-1][j-1]])//左
    }
}

if(dp[0][1])
    puts("impossible");
else
    cout<<dp[0][1]<<endl;

完整ac碼

#include <iostream>
#include <stdio.h>
#include <string.h>
using namespace std;
const int INF=0x3f3f3f3f;
int t[50+10]；
int dp[200+10][50+10]；
int has_train[200+10][50+10][2];

int main()
{
    int n,T,M1,M2,flag;
    int casen=0;
    while(scanf("%d",&n)!=EOF&&n)
    {
        memset(has_train,0,sizeof(has_train));
        memset(t,0,sizeof(t));
        memset(dp,INF,sizeof(dp));
        scanf("%d",&T);
        for(int i=1; i<n; i++)
            scanf("%d",&t[i]);
        scanf("%d",&M1);
        for(int i=1; i<=M1; i++)
        {
            scanf("%d",&flag);
            for(int j=1; j<=n; j++)
            {
                flag+=t[j-1];
                has_train[flag][j][0]=1;
            }
        }
        scanf("%d",&M2);
        for(int i=1; i<=M2; i++)
        {
            scanf("%d",&flag);
            for(int j=n; j>=1; j--)
            {
                flag+=t[j];
                has_train[flag][j][1]=1;
            }
        }
        for(int i=1; i<=n-1; i++)
            dp[T][i]=INF;
        dp[T][n]=0;
        for(int i=T-1; i>=0; i--)
            for(int j=1; j<=n; j++)
            {
                dp[i][j]=dp[i+1][j]+1;
                if(j<n&&has_train[i][j][0]&&i+t[j]<=T)
                    dp[i][j]=min(dp[i][j],dp[i+t[j]][j+1]);
                if(j>1&&has_train[i][j][1]&&i+t[j-1]<=T)
                    dp[i][j]=min(dp[i][j],dp[i+t[j-1]][j-1]);
            }
        cout<<"Case Number "<<++casen<<": ";
        if(dp[0][1]>=INF)
            puts("impossible");
        else
            cout<<dp[0][1]<<endl;
    }
    return 0;
}

B - The Tower of Babylon

有n（n<=30)種立方體，每種都有無窮多個
要求選一些立方體，摞成一根盡量高的柱子(可以自行選擇哪一條作為高)
每個立方體的底面長寬分別嚴格小于它下方立方體的底面長寬

分析

任何時候都只有頂面（底=頂）尺寸會影響到后續決策，美增加一個立方體以后頂面長和寬都必須嚴格減小，所以這個圖也是DAG，可以套用最長路

由于只有三種面，每種立方體只要三個就夠了，每輸入一個立方體，就可以算作輸入了三個不同的立方體(任選一條邊作為高)，然后每一個立方體建邊，套用DAG上的dp模板

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 100+10;

int n;
int H[MAXN];//記錄立方體i的高
int d[MAXN];//記錄以i為起點的最大高度
int G[MAXN][MAXN];//記錄i是否可以作為j的底，存圖
int a[3];//3種邊長

struct Cube
{
    int x,y;//長和寬
} cube[MAXN];

void have_edge(int i,int j)//i是否可以作為j的底，可以則連邊
{ 
    if(cube[i].x>cube[j].x && cube[i].y>cube[j].y)
        G[i][j]=1;
}

int dp(int i)
{
    int &ans = d[i];
    if(ans > 0)
        return ans;
    ans = H[i];
    for(int j=0; j<3*n; j++)
        if(G[i][j])
            ans=max(ans,H[i]+dp(j));
    return ans;
}

int main()
{
    int casen = 0;
    while(scanf("%d",&n)!=EOF&&n)
    {
        int ans=0;
        memset(d,0,sizeof(d));
        memset(G,0,sizeof(G));
        for(int i=0; i<n; i++)
        {
            scanf("%d %d %d",&a[0],&a[1],&a[2]);
            sort(a,a+3);
            cube[3*i].x=a[0],cube[3*i].y=a[1],H[3*i]=a[2];
            cube[3*i+1].x=a[0],cube[3*i+1].y=a[2],H[3*i+1]=a[1];
            cube[3*i+2].x=a[1],cube[3*i+2].y=a[2],H[3*i+2]=a[0];
        }
        for(int i=0; i<3*n; i++)
            for(int j=0; j<3*n; j++)
                have_edge(i,j);
        for(int i=0; i<3*n; i++)
            dp(i);
        for(int i=0 ; i<3*n ; i++)
            ans=max(ans,d[i]);
        printf("Case %d: maximum height = %d\n",++casen ,ans);
    }
    return 0;
}

C - Tour

給定平面n個點(n≤1000)的坐標，按照x遞增的順序給出，保證各點的x都不同且都為正整數

你的任務是設計一條路線，從最左邊的點出發，嚴格向右走到達最右點再嚴格向左回到最左點，要求除了最左和最右，每個點恰好經過一次，輸出最短路徑長度

分析

從左到右再回來可以轉化成：兩個人同事從最左出發，沿著兩條不同的路徑走，最后到達最右點，并且除了起點和終點都只能有一個人經過，自然想到可以用d(i,j)表示：一個人走到i點，另一個人走到j，還需要走多長距離到達最右點
但是我們發現這樣狀態好像很難轉移，比如計算d(i,j)時，我們不知道能不能讓i上的1號同學走到i+1，因為從狀態里看不出來i+1有沒有被j上的2號同學走過，也就是說這個狀態定義的難以轉移

然后我們可以簡單修改一下定義，讓d(i,j)表示：1~max[d(i,j)]全部走過，且兩個人目前位置是i和j時，還需要走多長距離到達最右點，在這個定義下d(i,j)=d(j,i)，我們再規定始終有i>j，如果j>i了，只需要交換A、B的角色即可，即將i換為j，j換為i，這樣，不管是哪個人，下一步只能走到i＋1 , i＋2,…這些點

那么問題又來了，如果走到i＋2，情況變成了“走過1~ i 和 i＋2，但是i＋1沒走過”，不合法

那么直接ban了這個路不就可以了，也就是說，d(i,j)只允許其中一個人走到i＋1，而不能走到i＋2, i＋3,…
換句話說，狀態d(i,j)只能轉移到d(i＋1,j)和d(i＋1,i)，這里意思就是：如果第一個人直接走到了i＋2，那么它再也無法走到i＋1了，只能靠第二個人走到i＋1，既然如此，現在就讓第二個人走到i＋1

邊界是d(n－1,j) = dist(n－1,n)＋dist(j,n)，其中dist(a,b)表示點a和b之間的距離，因為根據定義，所有點都走過了，兩個人只需直接走到終點。所求結果是dist(1,2)＋d(2,1)，因為第一步一定是某個人走到了第二個點，根據定義，這就是d(2,1)

#include <bits/stdc++.h>
using namespace std;
const int MAXN=1000+10;
double d[MAXN][MAXN];//第一個走到i第二個人走到j時,還需要走多長距離走完
int n;

struct point
{
    int x, y;//坐標
}p[MAXN];

double dist(int A,int B)//p[A]到p[B]距離，隨便怎么實現，這里用hypot()
{
    int X = p[A].x - p[B].x;
    int Y = p[A].y - p[B].y;
    return hypot(X, Y);
}

double dp(int i, int j)//i>j
{
    double& ans = d[i][j];
    if (ans > 0)
        return ans;
    if (i == n - 1)
        return ans = dist(i, n) + dist(j, n);
    ans = min(dp(i + 1, j) + dist(i + 1, i), dp(i + 1, i) + dist(i + 1, j));
    return ans;
}

int main()
{
    while (cin >> n)
    {
        memset(d, 0, sizeof(d));
        for (int i = 1; i <= n; i++)
            cin >> p[i].x >> p[i].y;
        dp(2, 1);
        printf("%.2f\n", dist(2, 1) + d[2][1]);
    }
    return 0;
}

感謝各位的閱讀！關于“DAG上DP的示例分析”這篇文章就分享到這里了，希望以上內容可以對大家有一定的幫助，讓大家可以學到更多知識，如果覺得文章不錯，可以把它分享出去讓更多的人看到吧！