編程技術中冒泡排序、快速排序和堆排序的時間復雜度是多少

這篇文章主要介紹編程技術中冒泡排序、快速排序和堆排序的時間復雜度是多少，文中介紹的非常詳細，具有一定的參考價值，感興趣的小伙伴們一定要看完！

冒泡排序的時間復雜度：最好情況是“O(n)”，最壞情況是“O(n2)”。快速排序的的時間復雜度：最好情況是“O(nlogn)”，最壞情況是“O(n2)”。堆排序的時間復雜度是“O(nlogn)”。

本教程操作環境：windows7系統、Dell G3電腦。

冒泡排序（Bubble Sort）

時間復雜度

最好的情況：數組本身是順序的，外層循環遍歷一次就完成O(n)

最壞的情況：數組本身是逆序的，內外層遍歷O(n2)

空間復雜度
開辟一個空間交換順序O(1)
穩定性
穩定，因為if判斷不成立，就不會交換順序，不會交換相同元素

• 冒泡排序它在所有排序算法中最簡單。然而， 從運行時間的角度來看，冒泡排序是最差的一個，它的復雜度是O(n2)。

• 冒泡排序比較任何兩個相鄰的項，如果第一個比第二個大，則交換它們。元素項向上移動至正確的順序，就好像氣泡升至表面一樣，冒泡排序因此得名。

• 交換時，我們用一個中間值來存儲某一交換項的值。其他排序法也會用到這個方法，因此我 們聲明一個方法放置這段交換代碼以便重用。使用ES6（ECMAScript 2015）**增強的對象屬性——對象數組的解構賦值語法，**這個函數可以寫成下面 這樣：

[array[index1], array[index2]] = [array[index2], array[index1]];

具體實現：

function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {//外循環（行{2}）會從數組的第一位迭代 至最后一位，它控制了在數組中經過多少輪排序
    for (let j = 0; j < arr.length - i; j++) {//內循環將從第一位迭代至length - i位，因為后i位已經是排好序的，不用重新迭代
      if (arr[j] > arr[j + 1]) {//如果前一位大于后一位
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];//交換位置
      }
    }
  }
  return arr;
}

快速排序

時間復雜度
最好的情況：每一次base值都剛好平分整個數組，O(nlogn)
最壞的情況：每一次base值都是數組中的最大/最小值，O(n2)

空間復雜度
快速排序是遞歸的，需要借助棧來保存每一層遞歸的調用信息，所以空間復雜度和遞歸樹的深度一致
最好的情況：每一次base值都剛好平分整個數組，遞歸樹的深度O(logn)
最壞的情況：每一次base值都是數組中的最大/最小值，遞歸樹的深度O(n)

穩定性
快速排序是不穩定的，因為可能會交換相同的關鍵字。
快速排序是遞歸的，
特殊情況：left>right,直接退出。

步驟：

(1) 首先，從數組中選擇中間一項作為主元base，一般取第一個值。

(2) 創建兩個指針，左邊一個指向數組第一個項，右邊一個指向數組最后一個項。移動右指針直到找到一個比主元小的元素，接著，移動左指 針直到我們找到一個比主元大的元素，然后交 換它們，重復這個過程，直到左指針遇見了右指針。這個過程將使得比主元小的值都排在主元之前，而比主元大的值都排在主元之后。這一步叫作劃分操作。

(3)然后交換主元和指針停下來的位置的元素（等于說是把這個元素歸位，這個元素左邊的都比他小，右邊的都比他大，這個位置就是他最終的位置）

(4) 接著，算法對劃分后的小數組（較主元小的值組成的子數組，以及較主元大的值組成的 子數組）重復之前的兩個步驟(遞歸方法），

遞歸的出口為left/right=i，也就是：

left>i-1 / i+1>right

此時，子數組數組已排序完成。

歸位示意圖：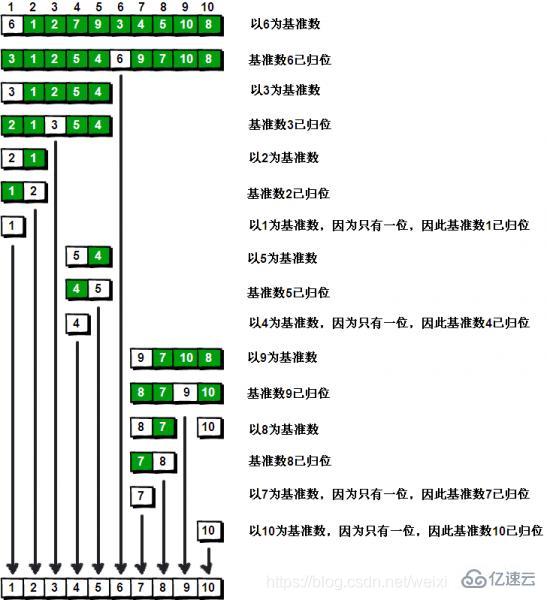

具體實現：

function quicksort(arr, left, right) {
  if (left > right) {
    return;
  }
  var i = left,
    j = right,
    base = arr[left]; //基準總是取序列開頭的元素
  //   var [base, i, j] = [arr[left], left, right]; //以left指針元素為base
  while (i != j) {
    //i=j，兩個指針相遇時，一次排序完成，跳出循環
    // 因為每次大循環里面的操作都會改變i和j的值，所以每次循環/操作前都要判斷是否滿足i<j
    while (i < j && arr[j] >= base) {
      //尋找小于base的右指針元素a，跳出循環，否則左移一位
      j--;
    }
    while (i < j && arr[i] <= base) {
      //尋找大于base的左指針元素b，跳出循環，否則右移一位
      i++;
    }
    if (i < j) {
      [arr[i], arr[j]] = [arr[j], arr[i]]; //交換a和b
    }
  }
  [arr[left], arr[j]] = [arr[j], arr[left]]; //交換相遇位置元素和base，base歸位
  //   let k = i;
  quicksort(arr, left, i - 1); //對base左邊的元素遞歸排序
  quicksort(arr, i + 1, right); //對base右邊的元素遞歸排序
  return arr;
}

參考：https://www.cnblogs.com/venoral/p/5180439.html

堆排序

堆的概念

• 堆是一個完全二叉樹。

• 完全二叉樹： 二叉樹除開最后一層，其他層結點數都達到最大，最后一層的所有結點都集中在左邊（左邊結點排列滿的情況下，右邊才能缺失結點）。

• 大頂堆：根結點為最大值，每個結點的值大于或等于其孩子結點的值。

• 小頂堆：根結點為最小值，每個結點的值小于或等于其孩子結點的值。

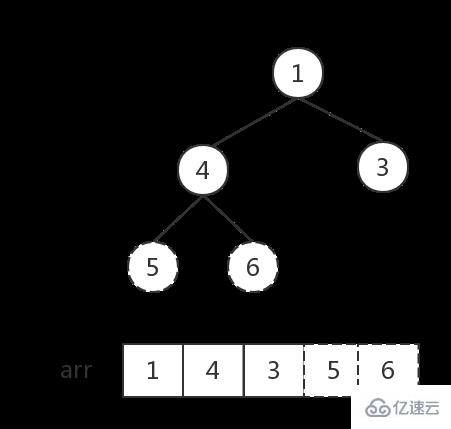
• 堆的存儲： 堆由數組來實現，相當于對二叉樹做層序遍歷。如下圖：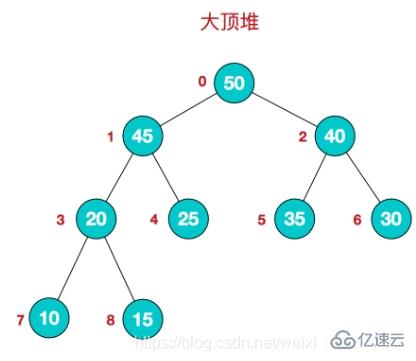
  
  

時間復雜度
總時間為建堆時間+n次調整堆 —— O(n)+O(nlogn)=O(nlogn)
建堆時間：從最后一個非葉子節點遍歷到根節點，復雜度為O(n)
n次調整堆：每一次調整堆最長的路徑是從樹的根節點到葉子結點，也就是樹的高度logn，所以每一次調整時間復雜度是O(logn)，一共是O(nlogn)

空間復雜度
堆排序只需要在交換元素的時候申請一個空間暫存元素，其他操作都是在原數組操作，空間復雜度為O(1)

穩定性
堆排序是不穩定的，因為可能會交換相同的子結點。

步驟一：建堆

• 以升序遍歷為例子，需要先將將初始二叉樹轉換成大頂堆，要求滿足：樹中任一非葉子結點大于其左右孩子。

• 實質上是調整數組元素的位置，不斷比較，做交換操作。

• 找到第一個非葉子結點——Math.floor(arr.length / 2 - 1)，從后往前依次遍歷

• 對每一個結點，檢查結點和子結點的大小關系，調整成大根堆

// 建立大頂堆
function buildHeap(arr) {
  //從最后一個非葉子節點開始，向前遍歷，
  for (let i = Math.floor(arr.length / 2 - 1); i >= 0; i--) {
    headAdjust(arr, i, arr.length); //對每一個節點都調整堆，使其滿足大頂堆規則
  }
}

步驟二：調整指定結點形成大根堆

• 建立childMax指針指向child最大值節點，初始值為2 * cur + 1，指向左節點

• 當左節點存在時（左節點索引小于數組length），進入循環，遞歸調整所有節點位置，直到沒有左節點為止（cur指向一個葉結點為止），跳出循環，遍歷結束

• 每次循環，先判斷右節點存在時，右節點是否大于左節點，是則改變childMax的指向

• 然后判斷cur根節點是否大于childMax，

• 大于的話，說明滿足大頂堆規律，不需要再調整，跳出循環，結束遍歷

• 小于的話，說明不滿足大頂堆規律，交換根節點和子結點，

• 因為交換了節點位置，子結點可能會不滿足大頂堆順序，所以還要判斷子結點然后，改變cur和childMax指向子結點，繼續循環判斷。

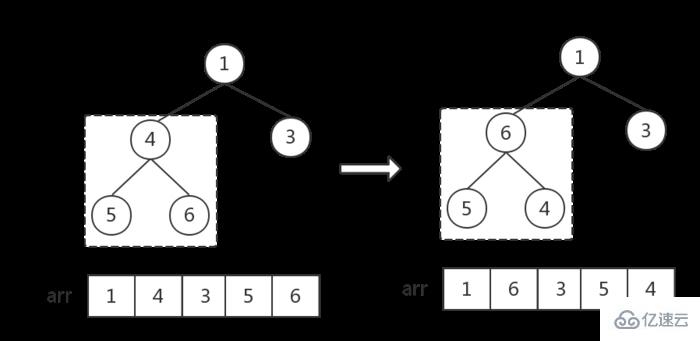
//從輸入節點處調整堆
function headAdjust(arr, cur, len) {
  let intialCur = arr[cur]; //存放最初始的
  let childMax = 2 * cur + 1; //指向子樹中較大的位置，初始值為左子樹的索引

  //子樹存在（索引沒超過數組長度）而且子樹值大于根時，此時不符合大頂堆結構，進入循環，調整堆的結構
  while (childMax < len) {
    //判斷左右子樹大小,如果右子樹更大，而且右子樹存在，childMax指針指向右子樹
    if (arr[childMax] < arr[childMax + 1] && childMax + 1 < len) childMax++;
    //子樹值小于根節點，不需要調整，退出循環
    if (arr[childMax] < arr[cur]) break;
    //子樹值大于根節點，需要調整，先交換根節點和子節點
    swap(arr, childMax, cur);
    cur = childMax; //根節點指針指向子節點，檢查子節點是否滿足大頂堆規則
    childMax = 2 * cur + 1; //子節點指針指向新的子節點
  }
}

步驟三：利用堆進行排序

• 從后往前遍歷大頂堆（數組），交換堆頂元素a[0]和當前元素a[i]的位置，將最大值依次放入數組末尾。

• 每交換一次，就要重新調整一下堆，從根節點開始，調整根節點～i-1個節點（數組長度為i），重新生成大頂堆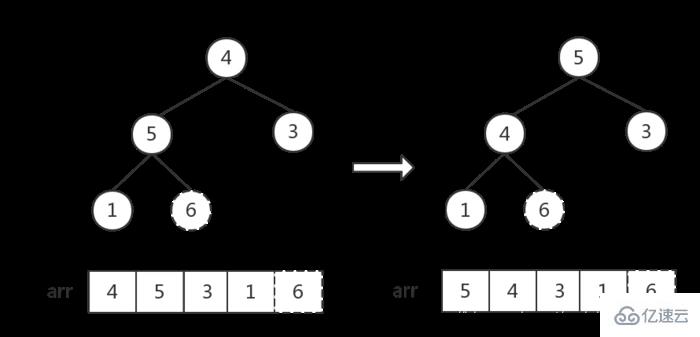
  
  

// 堆排序
function heapSort(arr) {
  if (arr.length <= 1) return arr;
  //構建大頂堆
  buildHeap(arr);
  //從后往前遍歷，
  for (let i = arr.length - 1; i >= 0; i--) {
    swap(arr, i, 0); //交換最后位置和第一個位置（堆頂最大值）的位置
    headAdjust(arr, 0, i); //調整根節點～i-1個節點，重新生成大頂堆
  }
  return arr;
}

完整代碼：

// 交換數組元素
function swap(a, i, j) {
  [a[i], a[j]] = [a[j], a[i]];
}
//從輸入節點處調整堆
function headAdjust(arr, cur, len) {
  let intialCur = arr[cur]; //存放最初始的
  let childMax = 2 * cur + 1; //指向子樹中較大的位置，初始值為左子樹的索引

  //子樹存在（索引沒超過數組長度）而且子樹值大于根時，此時不符合大頂堆結構，進入循環，調整堆的結構
  while (childMax < len) {
    //判斷左右子樹大小,如果右子樹更大，而且右子樹存在，childMax指針指向右子樹
    if (arr[childMax] < arr[childMax + 1] && childMax + 1 < len) childMax++;
    //子樹值小于根節點，不需要調整，退出循環
    if (arr[childMax] < arr[cur]) break;
    //子樹值大于根節點，需要調整，先交換根節點和子節點
    swap(arr, childMax, cur);
    cur = childMax; //根節點指針指向子節點，檢查子節點是否滿足大頂堆規則
    childMax = 2 * cur + 1; //子節點指針指向新的子節點
  }
}
// 建立大頂堆
function buildHeap(arr) {
  //從最后一個非葉子節點開始，向前遍歷，
  for (let i = Math.floor(arr.length / 2 - 1); i >= 0; i--) {
    headAdjust(arr, i, arr.length); //對每一個節點都調整堆，使其滿足大頂堆規則
  }
}
// 堆排序
function heapSort(arr) {
  if (arr.length <= 1) return arr;
  //構建大頂堆
  buildHeap(arr);
  //從后往前遍歷，
  for (let i = arr.length - 1; i >= 0; i--) {
    swap(arr, i, 0); //交換最后位置和第一個位置（堆頂最大值）的位置
    headAdjust(arr, 0, i); //調整根節點～i-1個節點，重新生成大頂堆
  }
  return arr;
}

以上是“編程技術中冒泡排序、快速排序和堆排序的時間復雜度是多少”這篇文章的所有內容，感謝各位的閱讀！希望分享的內容對大家有幫助，更多相關知識，歡迎關注億速云行業資訊頻道！