您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
樹: 非線性結構
1 樹是n(n>=0)個元素的集合
n=0時,稱為空樹
樹只有一個特殊的節點是沒有前驅元素的,稱為樹的根,及Root
樹中除了根節點外,其余的元素只能有一個前驅,可以有0個或多個后繼,根沒有前驅,只有后繼
2 遞歸定義
樹T 是n(n>=0)個元素的集合,n=0時,稱為空樹
其有且只有一個特殊元素及根,剩余的元素都可以被劃分為m個互不相交的集合,T1,T2,T3...Tm,而每個集合都是樹,稱為T的子樹subtree,其子樹也有自己的根
前驅: 當前節點前面的元素
后驅: 當前節點后面的元素
結點: 樹中的數據元素
節點的度degree:節點擁有的子樹的數目稱為度,記做d(v)
葉子結點: 結點的度為0,稱為葉子結點,終端結點,末端結點
分支結點:結點的度不為0,稱為非終端結點或分支結點
分支:結點之間的關系,及連線
內部結點:除根節點以外的分支結點,當然不包括葉子節點,及掐頭,去尾,留中間
樹的度: 樹的度是各個節點的度的最大值。
孩子(兒子child)結點:結點的子樹的根節點稱為該結點的孩子
雙親(父Parent)結點:一個結點是它各子樹的根結點的雙親。
兄弟(sibling)結點:具有相同雙親結點的結點
祖先結點:從根結點到該結點所經分支上的所有結點
子孫結點:結點所有子樹上的結點都稱為子孫
結點的層次:根結點為第一層,根結點的孩子為第二層,依次類推,記做L(v)
樹的深度(高度Depth):樹的層次的最大值
堂兄弟:雙親在同一層的結點。有序樹:結點的子樹是有序的(兄弟有大小,有先后次序),不能交換
無序樹:結點的子樹是無序的,可以交換
路徑:樹中的K個節點n1,n2...nk,滿足ni是n(i+1)的雙親,稱為n1到nk的一條路徑,就是一條線串下來的,前一個都是后一個的父(前驅)節點
路徑長度=路徑上結點長度-1,及分支數
森林:m(m>=0)棵不相交的樹的集合
對于結點而言,其子樹的集合就是森林,
1 唯一的根
2 子樹不相交
3 除了根以外,每個元素只能有一個前驅,可以有0個或多個后繼
4 根結點沒有雙親節點(前驅),葉子節點沒有孩子結點(后繼)
5 vi是vj的雙親,則L(vi)=L(vj)-1,也就是說雙親比孩子節點的層次小1
1 每個結點最多2個子樹
二叉樹不存在度數大于2的節點
2 它是有序樹,左子樹,右子樹是順序的,不能交換次序
3 即使某一個結點只有一顆子樹,也要確定其是左子樹還是右子樹
1 空二叉樹
2 只有一個根結點
3 根結點只有左子樹
4 根結點只有右子樹
5 根結點有左子樹和右子樹
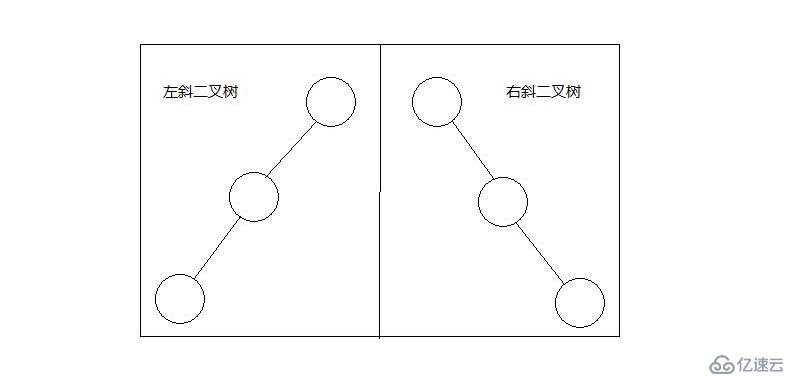
左斜樹:所有結點都只有左子樹
右斜樹:所有結點都只有右子樹
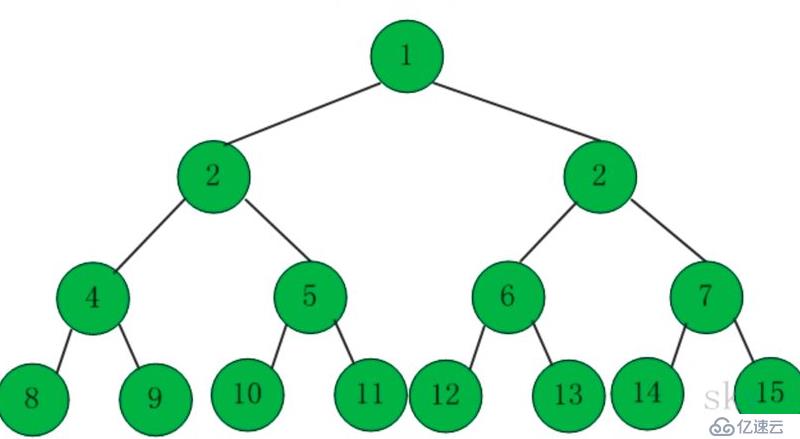
一顆二叉樹的所有分支結點都存在左子樹和右子樹,且所有葉子節點都只存在在最下面一層。
同樣深度的二叉樹,滿二叉樹節點最多
k為深度(1<=k<=n),則節點總數為 2**(k)-1
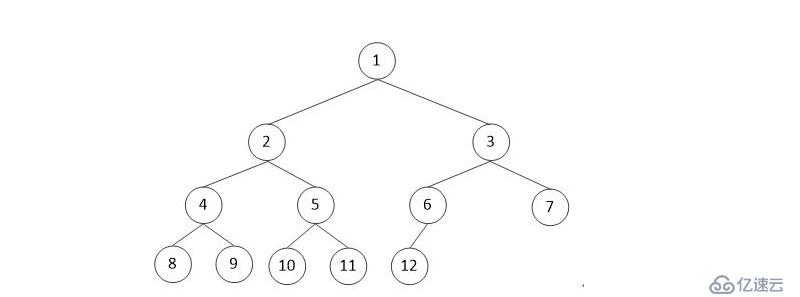
若二叉樹的深度為k,二叉樹的層數從1到k-1層的結點都打到了最大個數,在第k層的所有結點都集中在最左邊,這就是完全二叉樹
完全二叉樹由滿二叉樹引出
滿二叉樹一定是完全二叉樹,但完全二叉樹不一定是滿二叉樹
k為深度(1<=k<=n),則結點總數最大值為2**k-1,當達到最大值的時候就是滿二叉樹
1 在二叉樹中的第i層上最多有2**i-1 個節點(i>=1)
2 深度為k的二叉樹,至多有2**k -1個節點(k>=1)
3 對于任何一顆二叉樹T,如果其終點節點數為n0,度數為2的節點為n2,則有n0=n2+1,及葉子結點數-1=度數為2的節點數。
證明:
總結點數為n=n0+n1+n2,其中n0為度數為0的節點,及葉子節點的數量,n1為度數為1 的節點的數量,n2為節點為2度數的數量。
一棵樹的分支數為n-1,因為除了根節點外,其余結點都有一個分支,及n0+n1+n2-1
分支數還等于n0*0+n1*1+n2*2及 n1+2n2=n-1
可知 2*n2+n1=n0+n1+n2-1 及就是 n2=n0-1
4 高度為k的二叉樹,至少有k個節點
5 具有n個節點的完全二叉樹的深度為int(log2n)+1 或者 math.ceil(log2(n+1))6 有一個n個節點的完全二叉樹, 結點按照層序編號,如圖

如果i=1,則節點i是二叉樹的根,無雙親,如果i>1,則其雙親為int(i/2),向下取整。就是葉子節點的編號整除2得到的就是父節點的編號,如果父節點是i,則左孩子是2i,若有右孩子,則右孩子是2i+1,。
如果2i>n,則結點i無左孩子,及結點為葉子結點,否則其左孩子節點存在編號為2i。如果2i+1>n,則節點i無右孩子,此處未說明是否不存在左孩子,否則右孩子的節點存在編號為2i+1。
遍歷: 及對樹中的元素不重復的訪問一遍,又稱為掃描
一次將一層全部拿完,層序遍歷
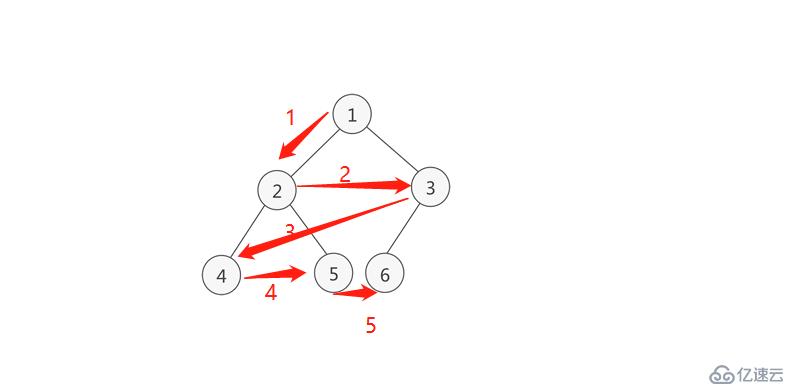
及 1 2 3 4 5一層一層的從左向右拿取
設樹的根結點為D,左子樹為L,右子樹為R。且要求L一定要在R之前,則有下面幾種遍歷方式
1 前序遍歷,也叫先序遍歷,也叫先跟遍歷,DLR 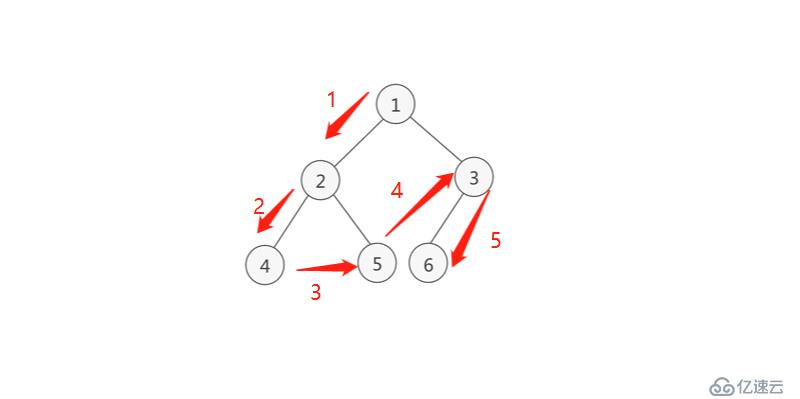
1-2-4-5-3-6
2 中序遍歷,也叫中跟遍歷, LDR 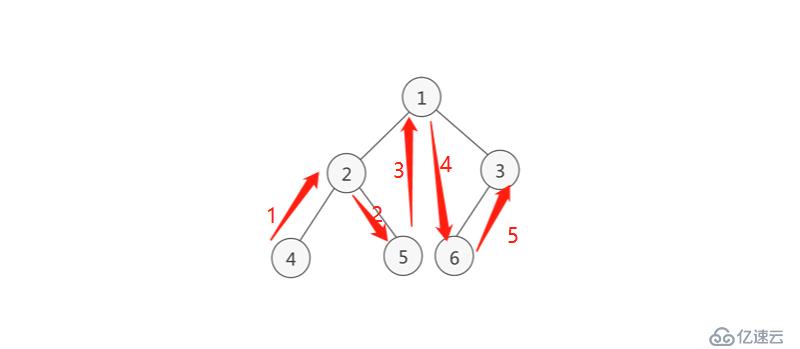
4-2-5-1-6-3
3 后序遍歷,也叫后跟遍歷,LRD 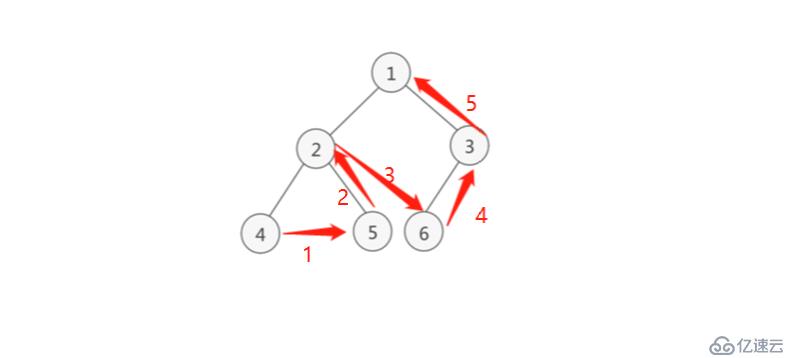
4-5-2-6-3-1
1 堆heap 是一個完全二叉樹
2 每個非葉子結點都要大于或等于其左右孩子結點的值稱為大頂堆
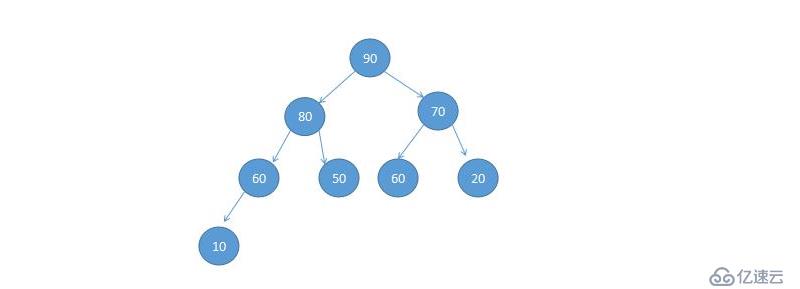
3 每個非葉子結點都要小于或者等于其左右孩子結點的值稱為小頂堆
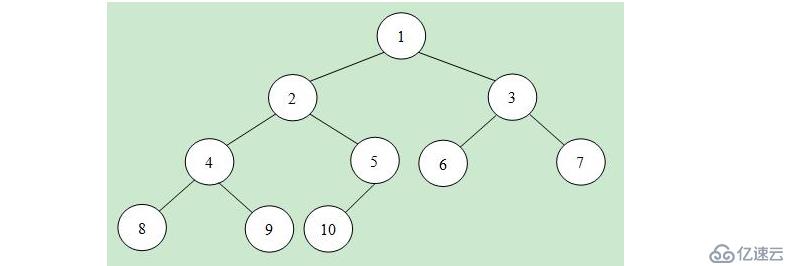
4 根節點一定是大頂堆的最大值,小頂堆中的最小值
1 待排序數字為 49 38 65 97 76 13 27 49
2 構建一個完全二叉樹存放數據,并根據性質5對元素進行編號,放入順序的數據結構中
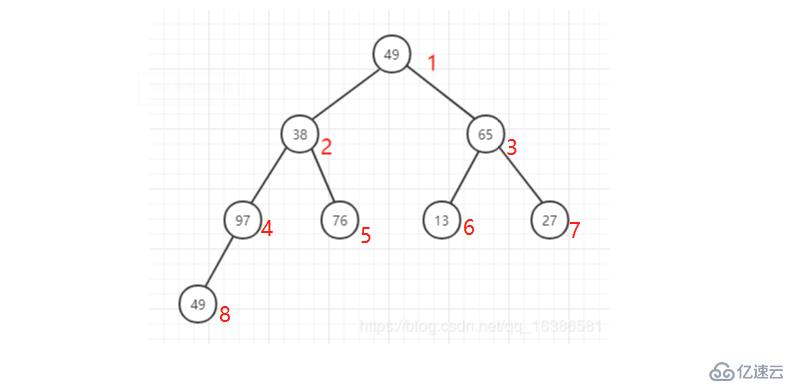
3 構造一個列表為 [0,49,38,65,97,76,13,27,49]的列表
1 度數為2的結點,如果他的左右孩子最大值比它大,則將這個值和該節點交換
2 度數為1 的結點,如果它的左孩子的值大于它,則交換
3 如果節點被置換到新的位置,則還需要和其孩子節點重復上述過程
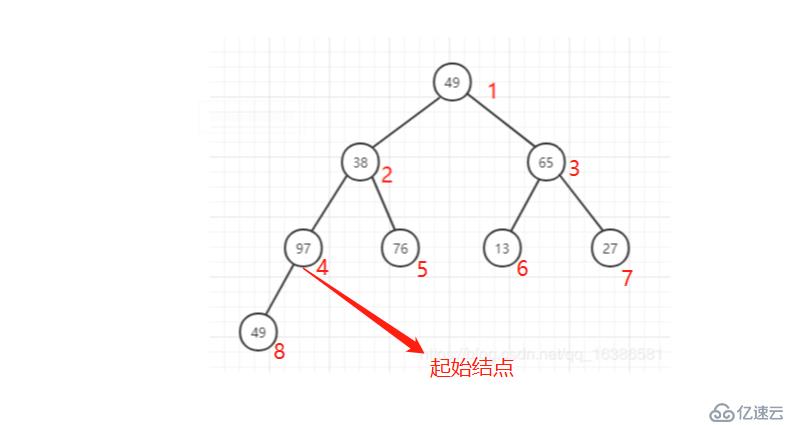
1 從完全二叉樹的最后一個結點的雙親開始,及最后一層的最右邊的葉子結點的父結點開始
2 結點數為n,則起始節點的編號為n//2(及最后一個結點的父節點)
從起始節點開始向左尋找其同層節點,到頭后再從上一層的最右邊節點開始繼續向左逐步查找,直到根節點
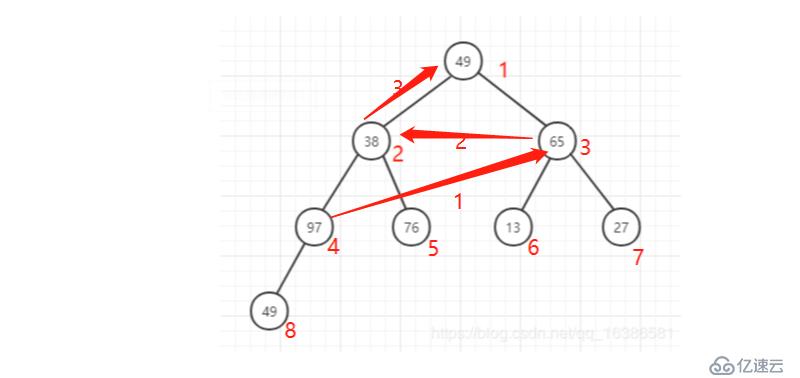
5 大頂堆目標
確保每個結點的都比其左右結點的值大
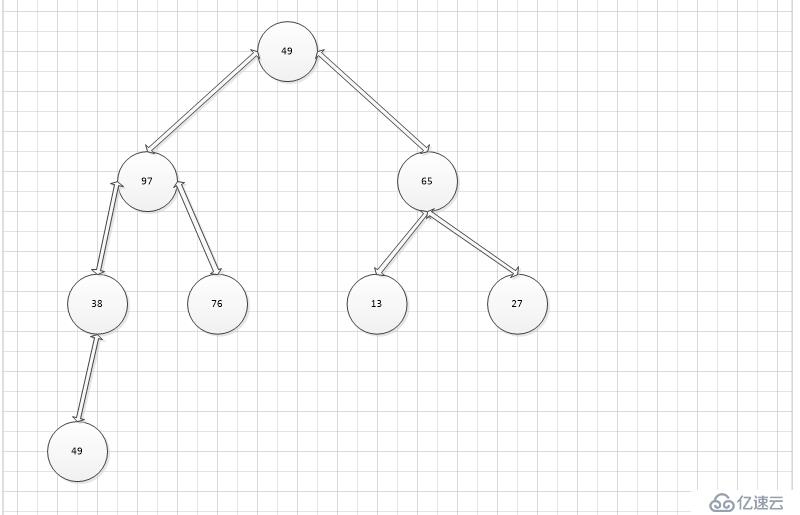
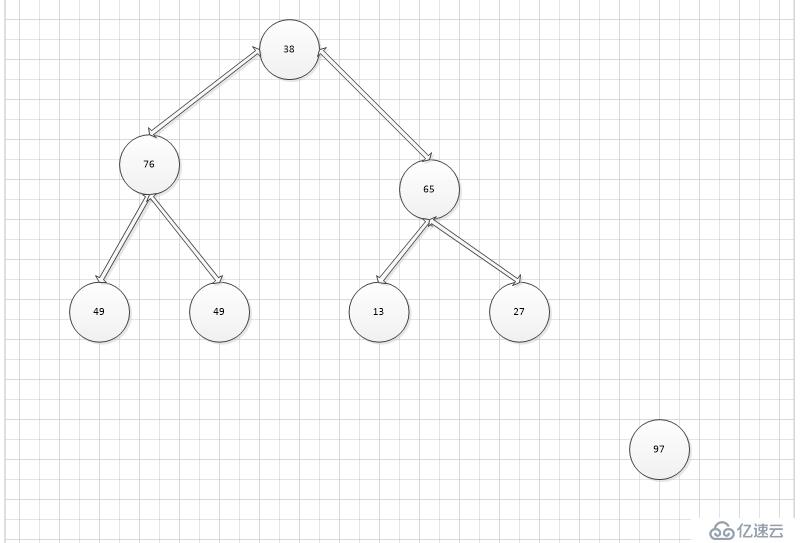
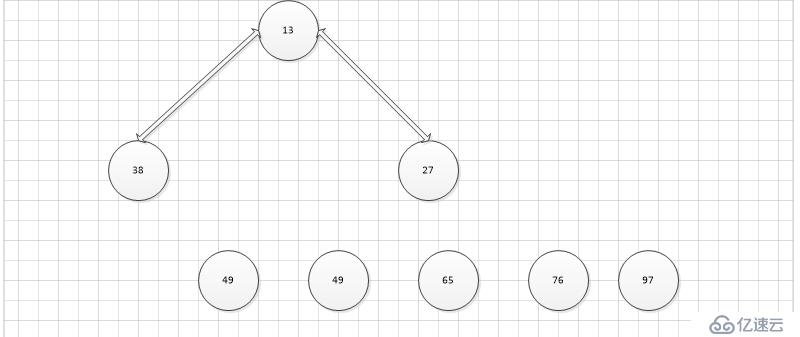
第一步,調換97和38,保證跟大
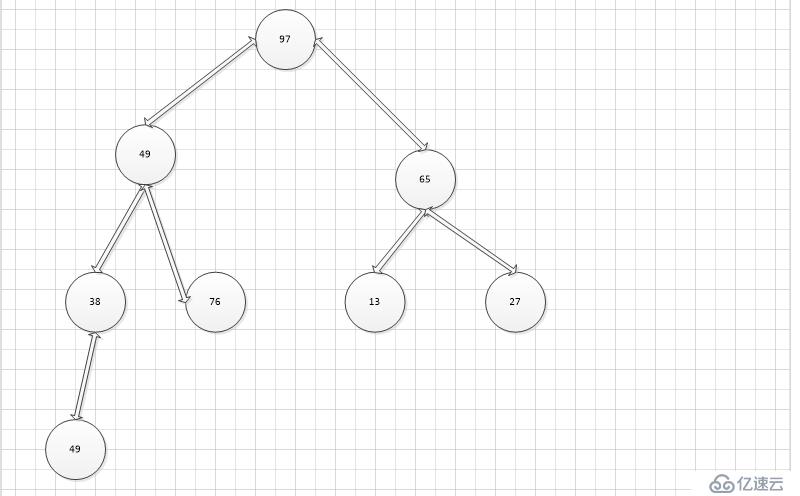
第二步,調換49和97
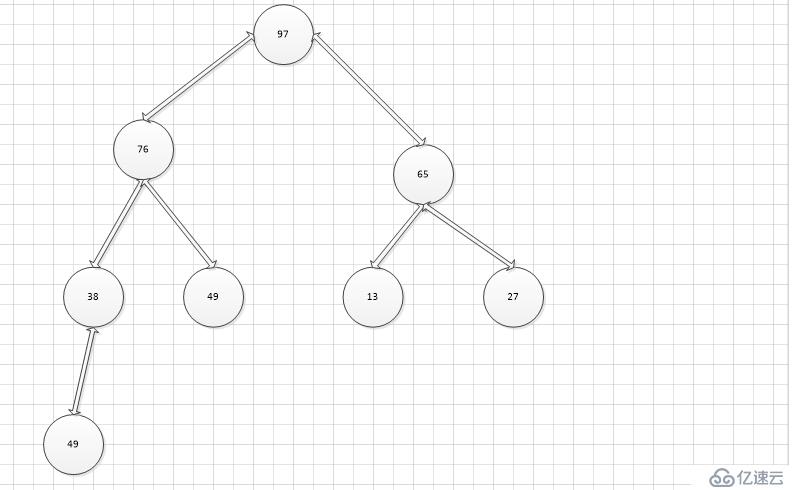
第三步,調換76和49
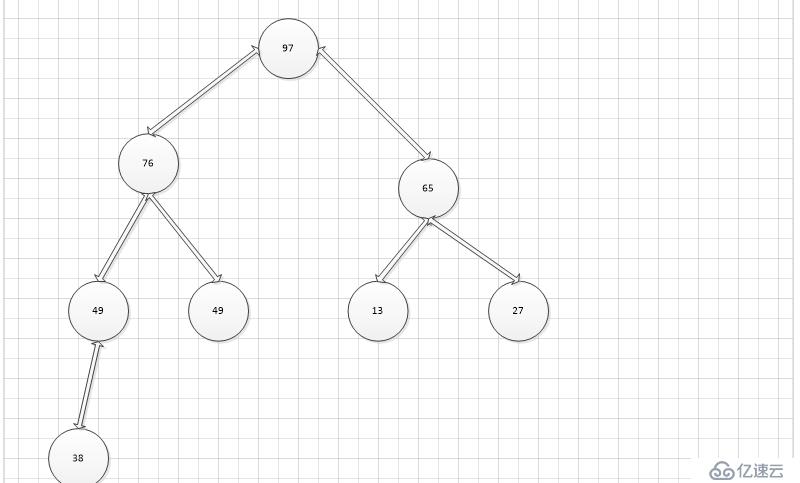
第四步,調換38和49
此時大頂堆的構建已經完成
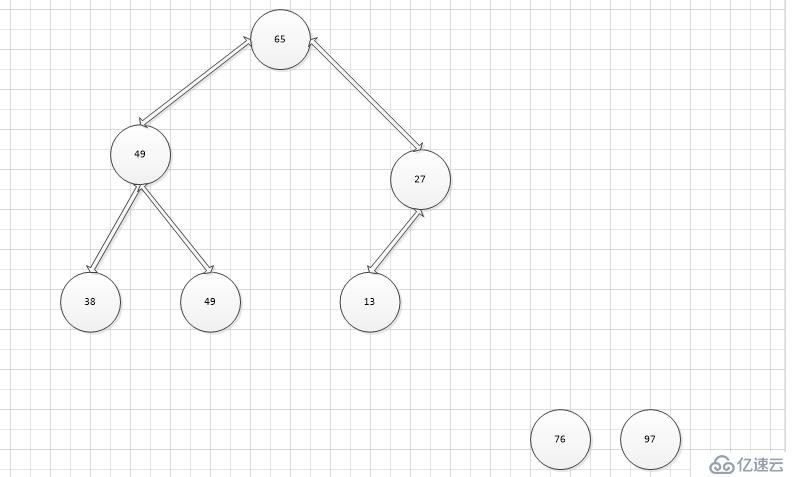
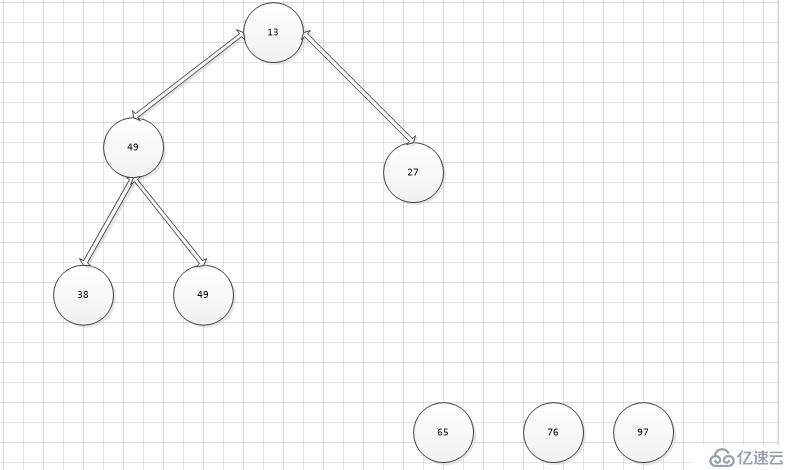
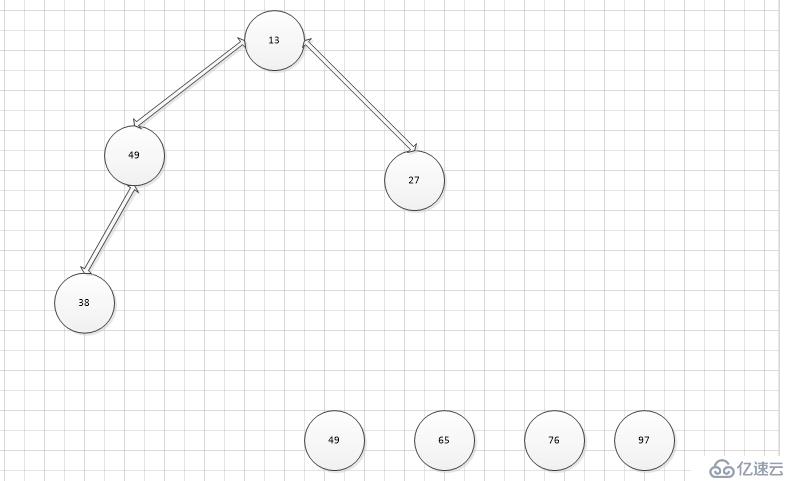
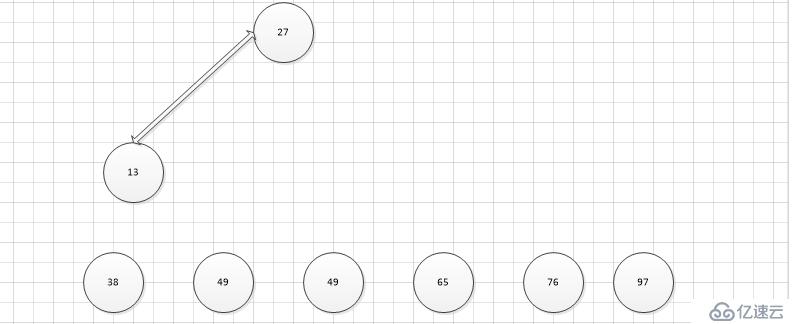
將大頂堆根節點這個最大值和最后一個葉子節點進行交換,則最后一個葉子節點成為了最大值,將這個葉子節點排除在待排序節點之外,并從根節點開始,重新調整為大頂堆,重復上述步驟。

l1=[1,2,3,4,5,6,7,8,9]
打印結果應當如下

思路:可通過將其數字映射到下方的一條線上的方式進行處理及就是 8 4 9 2 0 5 0 1 0 6 0 3 0 7 0 的數字,其之間的空格可以設置為一個空格的長度,其數字的長度也可設置為固定的2,則
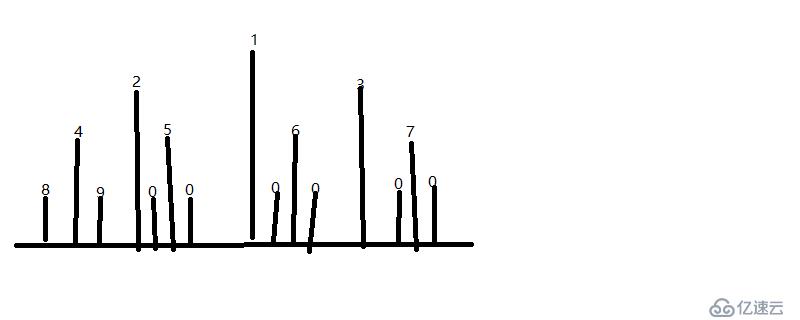
則第一層第一個數字據前面的空格個數為7個,據后面的空格也是7個,
第二層第一個數字據前面的空格個數為3個,第二個數字距離后面的空格也是3個,
第三層據前面的空格為1,第三層最后一個據后面的空格也是1,
第四層據前面的空格是0,第四層最后一個據后面的空格也是0,
現在在其標號前面從1開始,則層數和空格之間的關系是1 7
2 3
3 1
4 0
轉換得到
4 7
3 3
2 1
1 0及就是 2**(l-1) -1 l 表示層數
間隔關系如下
1 0
2 8
3 4
4 2
轉換得到
4 0
3 8
2 4
1 2
及就是 2**l其中l 表示層數。
代碼如下
import math
# 打印二叉樹
def t(list):
'''
層數 層數取反(depth+1-i,depth表示總層數,此處為4,i表示層數) 據前面的空格數 間隔數 每層字數為
1 4 7 0 1
2 3 3 7 2
3 2 1 3 4
4 1 0 1 8
(2**(depth-i)-1) (2**(depth-i)-1) (2**i)
層數和數據長度的關系是 n表示的是數據長度
1 1
2-3 2
4-7 3
8-15 4
2**(i-1)<num<(2**i)-1,及就是int(log2n) +1 及 math.ceil(log2n)
'''
index=1
depth=math.ceil(math.log(len(list),2)) #此處獲取到的是此列表轉換成二叉樹的深度,此處前面插入了一個元素,保證列表和二叉樹一樣,其真實數據都是從1開始
sep=' ' # 此處表示數字的寬度
for i in range(depth):
offset=2**i #每層的數字數量1 2 4 8
print (sep*(2**(depth-i-1)-1),end="") # 此處取的是前面空格的長度
line=list[index:index+offset] #提取每層的數量
for j,x in enumerate(line):
print ("{:>{}}".format(x,len(sep)),end="") # 此處通過format來獲取其偏移情況,第一個x表示其大括號中的內容,第二個表示偏移的程度
interval= 0 if i ==0 else 2**(depth-i)-1 # 此處獲取到的是間隔數,當值大于1時,滿足如此表達式
if j < len(line)-1: #選擇最后一個時不打印最后一個的后面的空格,及就是1,3,7后面的空格
print (sep*interval,end="")
index += offset
print ()結果如下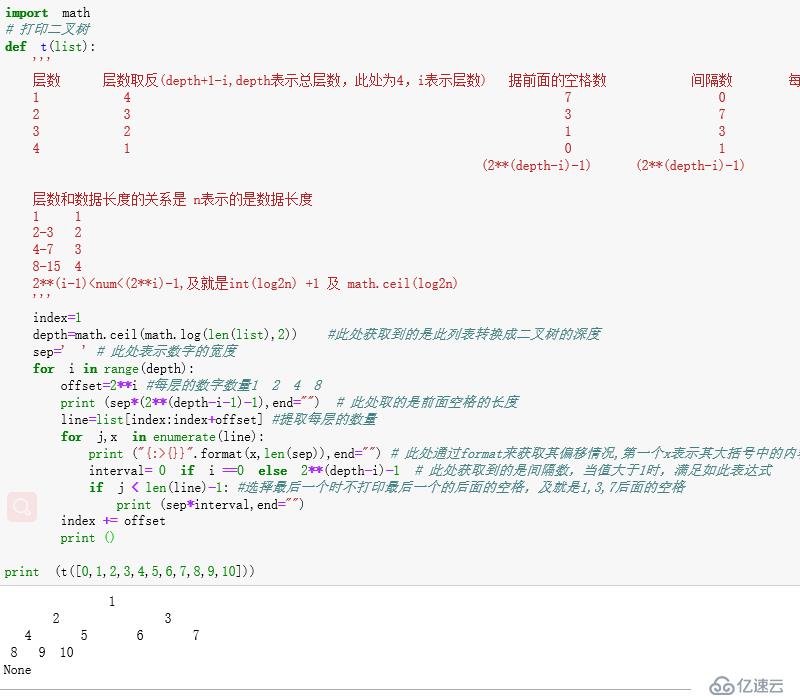
# 構建一個子樹的大頂堆
def heap_adjust(n,i,array):
'''
調整當前結點(核心算法)
調整的結點的起點在n//2(二叉樹性質5結論),保證所有調整的結點都有孩子結點
:param n : 待比較數個數
:param i : 當前結點下標
:param array : 待排序數據
:return : None
'''
while 2*i<=n: # 孩子結點判斷,2i為左孩子,2i+1為右孩子
lchile_index= 2*i #選擇結點起始并記錄 n=2*i-1,因為其是從0開始,因此只有len()-1
max_child_index=lchile_index
# 判斷左右孩子的大小,并將大的賦值給max_child_index
if n > lchile_index and array[lchile_index+1] > array[lchile_index]: #說明其有右孩子,且右孩子大于左孩子
max_child_index=lchile_index+1 #n=2i+1 # 此時賦值的是下標
# 判斷左右孩子的最大值和父結點比較,若左右結點的最大值大,則進行交換
if array[max_child_index] > array[i]: #此處的i是父節點,通過和父節點進行比較來確認其最大,
array[i],array[max_child_index]=array[max_child_index],array[i]
i= max_child_index #右子節點的下標會賦值到父結點,并將其值賦值到父結點,
else:
break
# 構建所有的大頂堆傳入參數
def max_heap(total,array):
for i in range(total//2,0,-1): #構建最后一個葉子結點的父結點
heap_adjust(total,i,array) #傳入總長和最后一個葉子結點的父結點和數列
print (t(array))
return array
#構建大頂堆,起點選擇
def sort(total,array): # 此處起點是1,因此必須在前面添加一個元素,以保證其位置編號和樹相同
while total>1:
max_heap(total,array)
array[1],array[total]=array[total],array[1] #將最后一個結點和第一個結點調換,
total-=1
return array結果如下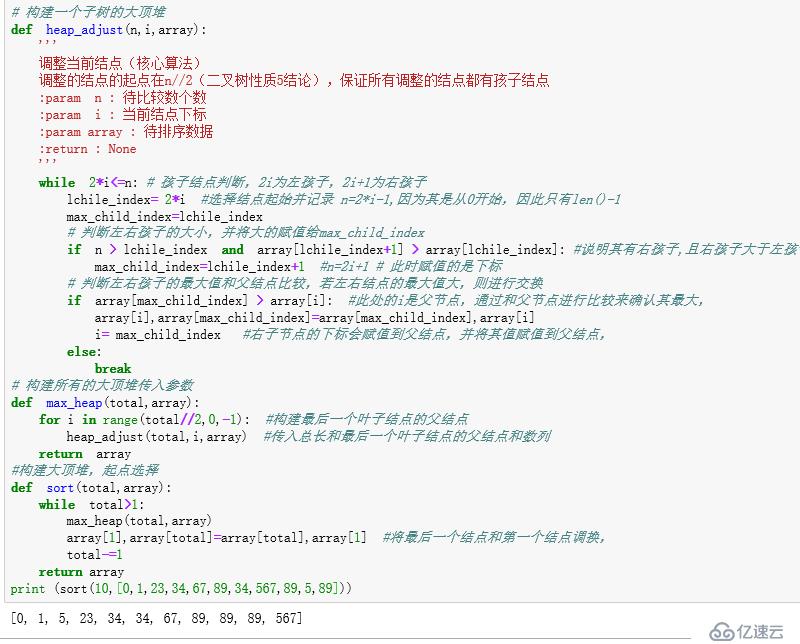
堆排序 Heap Sort 是利用堆性質的一種選擇排序,在堆頂選出最大值或最小值
時間復雜度
堆排序的時間復雜度為O(nlog2 n),由于堆排序對原始記錄的排序狀態不敏感,因此其無論是最好,最壞和平均時間復雜度均為O(nlog2 n)空間復雜度
只是使用了一個交換用的空間,其空間復雜度為O(1)
穩定性
不穩定的排序算法
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。