您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要講解了“C語言中二叉樹的常見操作是什么”,文中的講解內容簡單清晰,易于學習與理解,下面請大家跟著小編的思路慢慢深入,一起來研究和學習“C語言中二叉樹的常見操作是什么”吧!
一、基本概念
每個結點最多有兩棵子樹,左子樹和右子樹,次序不可以顛倒。
性質:
1、非空二叉樹的第n層上至多有2^(n-1)個元素。
2、深度為h的二叉樹至多有2^h-1個結點。
滿二叉樹:所有終端都在同一層次,且非終端結點的度數為2。
在滿二叉樹中若其深度為h,則其所包含的結點數必為2^h-1。
完全二叉樹:除了最大的層次即成為一顆滿二叉樹且層次最大那層所有的結點均向左靠齊,即集中在左面的位置上,不能有空位置。
對于完全二叉樹,設一個結點為i則其父節點為i/2,2i為左子節點,2i+1為右子節點。
二、存儲結構
順序存儲:
將數據結構存在一塊固定的數組中。
#define LENGTH 100
typedef char datatype;
typedef struct node{
datatype data;
int lchild,rchild;
int parent;
}Node;
Node tree[LENGTH];
int length;
int root;雖然在遍歷速度上有一定的優勢,但因所占空間比較大,是非主流二叉樹。二叉樹通常以鏈式存儲。
鏈式存儲:
typedef char datatype;
typedef struct BinNode{
datatype data;
struct BinNode* lchild;
struct BinNode* rchild;
}BinNode;
typedef BinNode* bintree; //bintree本身是個指向結點的指針三、二叉樹的遍歷
遍歷即將樹的所有結點訪問且僅訪問一次。按照根節點位置的不同分為前序遍歷,中序遍歷,后序遍歷。
前序遍歷:根節點->左子樹->右子樹
中序遍歷:左子樹->根節點->右子樹
后序遍歷:左子樹->右子樹->根節點
例如:求下面樹的三種遍歷
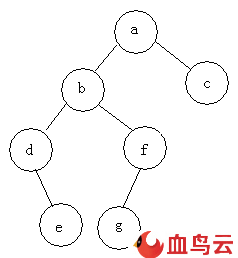
前序遍歷:abdefgc
中序遍歷:debgfac
后序遍歷:edgfbca
四、遍歷的實現
遞歸實現(以前序遍歷為例,其他的只是輸出的位置稍有不同)
void preorder(bintree t){
if(t){
printf("%c ",t->data);
preorder(t->lchild);
preorder(t->rchild);
}
}非遞歸的實現
因為當遍歷過根節點之后還要回來,所以必須將其存起來。考慮到后進先出的特點,選用棧存儲。數量確定,以順序棧存儲。
#define SIZE 100
typedef struct seqstack{
bintree data[SIZE];
int tag[SIZE]; //為后續遍歷準備的
int top; //top為數組的下標
}seqstack;
void push(seqstack *s,bintree t){
if(s->top == SIZE){
printf("the stack is full\n");
}else{
s->top++;
s->data[s->top]=t;
}
}
bintree pop(seqstack *s){
if(s->top == -1){
return NULL;
}else{
s->top--;
return s->data[s->top+1];
}
}1、前序遍歷
void preorder_dev(bintree t){
seqstack s;
s.top = -1; //因為top在這里表示了數組中的位置,所以空為-1
if(!t){
printf("the tree is empty\n");
}else{
while(t || s.stop != -1){
while(t){ //只要結點不為空就應該入棧保存,與其左右結點無關
printf("%c ",t->data);
push(&s,t);
t= t->lchild;
}
t=pop(&s);
t=t->rchild;
}
}
}2、中序遍歷
void midorder(bintree t){
seqstack s;
s.top = -1;
if(!t){
printf("the tree is empty!\n");
}else{
while(t ||s.top != -1){
while(t){
push(&s,t);
t= t->lchild;
}
t=pop(&s);
printf("%c ",t->data);
t=t->rchild;
}
}
}3、后序遍歷
因為后序遍歷最后還要要訪問根結點一次,所以要訪問根結點兩次。采取夾標志位的方法解決這個問題。
這段代碼非常糾結,對自己有信心的朋友可以嘗試獨立寫一下。反正我是寫了很長時間。邏輯不難,我畫了一張邏輯圖:
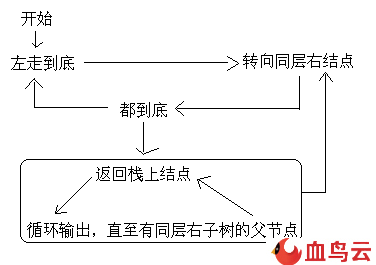
代碼:
void postorder_dev(bintree t){
seqstack s;
s.top = -1;
if(!t){
printf("the tree is empty!\n");
}else{
while(t || s.top != -1){ //棧空了的同時t也為空。
while(t){
push(&s,t);
s.tag[s.top] = 0; //設置訪問標記,0為第一次訪問,1為第二次訪問
t= t->lchild;
}
if(s.tag[s.top] == 0){ //第一次訪問時,轉向同層右結點
t= s.data[s.top]; //左走到底時t是為空的,必須有這步!
s.tag[s.top]=1;
t=t->rchild;
}else {
while (s.tag[s.top] == 1){ //找到棧中下一個第一次訪問的結點,退出循環時并沒有pop所以為其左子結點
t = pop(&s);
printf("%c ",t->data);
}
t = NULL; //必須將t置空。跳過向左走,直接向右走
}
}
}
}4、層次遍歷:即每一層從左向右輸出
元素需要儲存有先進先出的特性,所以選用隊列存儲。
隊列的定義:
#define MAX 1000
typedef struct seqqueue{
bintree data[MAX];
int front;
int rear;
}seqqueue;
void enter(seqqueue *q,bintree t){
if(q->rear == MAX){
printf("the queue is full!\n");
}else{
q->data[q->rear] = t;
q->rear++;
}
}
bintree del(seqqueue *q){
if(q->front == q->rear){
return NULL;
}else{
q->front++;
return q->data[q->front-1];
}
}遍歷實現
void level_tree(bintree t){
seqqueue q;
bintree temp;
q.front = q.rear = 0;
if(!t){
printf("the tree is empty\n");
return ;
}
enter(&q,t);
while(q.front != q.rear){
t=del(&q);
printf("%c ",t->data);
if(t->lchild){
enter(&q,t->lchild);
}
if(t->rchild){
enter(&q,t->rchild);
}
}
}5、利用前序遍歷的結果生成二叉樹
//遞歸調用,不存點,想的時候只關注于一個點,因為還會回來的,不要跟蹤程序運行,否則容易多加循環
void createtree(bintree *t){
datatype c;
if((c=getchar()) == '#')
*t = NULL;
else{
*t = (bintree)malloc(sizeof(BinNode));
(*t)->data = c;
createtree(&(*t)->lchild);
createtree(&(*t)->rchild);
}
}6、二叉樹的查找
bintree search_tree(bintree t,datatype x){
if(!t){
return NULL;
}
if(t->data == x){
return t;
}else{
if(!search_tree(t->lchild,x)){
return search_tree(t->rchild,x);
}
return t;
}
}7、統計結點個數
int count_tree(bintree t){
if(t){
return (count_tree(t->lchild)+count_tree(t->rchild)+1);
}
return 0;
}8、比較兩個樹是否相同
int is_equal(bintree t1,bintree t2){
if(!t1 && !t2){ //都為空就相等
return 1;
}
if(t1 && t2 && t1->data == t2->data){ //有一個為空或數據不同就不判斷了
if(is_equal(t1->lchild,t2->lchild))
if(is_equal(t1->rchild,t2->rchild)){
return 1;
}
}
return 0;
}9、求二叉樹的深度
int hight_tree(bintree t){
int h,left,right;
if(!t){
return 0;
}
left = hight_tree(t->lchild);
right = hight_tree(t->rchild);
h = (left>right?left:right)+1;
return h;
}感謝各位的閱讀,以上就是“C語言中二叉樹的常見操作是什么”的內容了,經過本文的學習后,相信大家對C語言中二叉樹的常見操作是什么這一問題有了更深刻的體會,具體使用情況還需要大家實踐驗證。這里是億速云,小編將為大家推送更多相關知識點的文章,歡迎關注!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。