如何實現js的雙線性插值和雙三次插值法

這篇文章主要介紹如何實現js的雙線性插值和雙三次插值法，文中介紹的非常詳細，具有一定的參考價值，感興趣的小伙伴們一定要看完！

在網頁中利用canvas進行繪圖時，遇到一個問題，原始的數據分辨率很小，而圖片要放大到整個網頁，所以需要把數據進行插值放大。學習了雙線性插值和三次內插法插值，兩種方式實現效果不同，都用js代碼實現了一下。

雙線性插值

原理

雙線性插值即在x和y兩個方向上，對數據各進行一次線性插值。
原始數據的矩陣，即一個二維數組，大小為a*b，目標矩陣大小為m*n，m、n比a、b可以大（放大），也可以小（縮小），當然比例也可以不一樣, 取決于你插值后的數據需要多大。
基本思想為，遍歷目標矩陣的坐標，如x*y這個點，找到這個點在原始矩陣中對應的位置，稱為映射點，然后找到這個映射點P在原始矩陣中周圍的四個點，然后根據映射點P到這個四個點的x和y方向上的坐標的距離，進行兩次線性插值，得到映射點的值即可。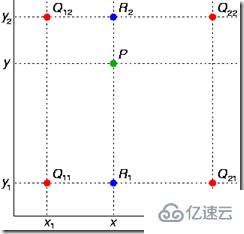

如上圖所示，p點為目標矩陣中x*y點在原始矩陣中映射的位置，它周圍最近的有Q12，Q11，Q21，Q22四個點，現在x方向進行線性插值，得到R1和R2兩個點的值，再在y方向進行一次線性插值，得到P點的值。
注意：用雙線性插值放大數據后，如果放大倍數過大，生成圖片后發現有著明顯的馬賽克現象
實現代碼參考后面js代碼

雙三次插值法

原理

雙三次插值又稱立方卷積插值。三次卷積插值是一種更加復雜的插值方式。該算法利用待采樣點周圍16個點的灰度值作三次插值，不僅考慮到4 個直接相鄰點的灰度影響，而且考慮到各鄰點間灰度值變化率的影響。具體的原理可參考下面博客：
參考這里的博客
基本原理就是，先找到目標矩陣中點在源數據矩陣中的映射點P，然后找到P點周圍16個點，然后根據P點坐標距離16個點的x和y方向的距離，利用BiCubic函數算出每個點的權重，最后每個點乘以權重后，加起來即可得到P的值。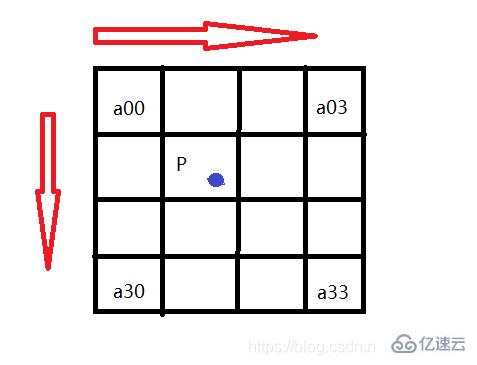

BiCubic函數：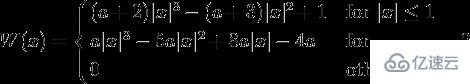

其中，a取-0.5時，BiCubic函數具有如下形狀：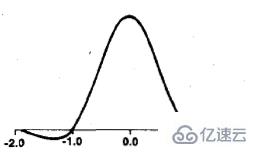

取a=-0.5時，放大的數據挺好，生成的圖片非常平滑，也保留了很多細節。
具體為什么要用這個函數，我也沒有深入研究，不過利用該方法放大數據后，生成圖片效果很好，沒有馬賽克現象

js實現

/**
 * 數據處理工具類（也可以自己直接定義方法，不用class）
 */class DataUtil {
	constructor() {}}/**
 * 數據插值
 * @param w 目標矩陣寬度
 * @param h 目標矩陣高度
 * @param data 源數據矩陣（二維數組）
 * @param type 插值方式，1：雙線性插值，2：雙三次插值法
 */DataUtil.scaleData = function(w, h, data, type = 2) {
	let t1 = new Date().getTime();
	let dw = data[0].length;
	let dh = data.length;
	
	let resData = new Array(h);
	
	for (let j = 0; j < h; j++) {
		let line = new Array(w);
		for (let i = 0; i < w; i++) {
			let v;
			if (type === 2) {
				// 雙三次插值法
				v = DataUtil.cubicInterpolation(w, h, i, j, data);
			} else if (type === 1) {
			    // 雙線性插值
				v = DataUtil.interpolation(w, h, i, j, data);
			} else {
				throw new Error('scale data, type not supported(type must be 1 or 2)');
			}
			line[i] = Math.round(v);
		}
		resData[j] = line;
	}
	
	let t2 = new Date().getTime();
	console.log("數據插值耗時:", (t2 - t1));
	
	return resData;}/**
 * 雙線性插值
 * @param sw 目標矩陣的寬度
 * @param sh 目標矩陣的高度
 * @param x_ 目標矩陣中的x坐標
 * @param y_ 目標矩陣中的y坐標
 * @param data 源數據矩陣（二維數組）
 */DataUtil.interpolation = function(sw, sh, x_, y_, data) {
	let t1 = new Date().getTime();
	let w = data[0].length;
	let h = data.length;
	
	let x = (x_ + 0.5) * w / sw - 0.5;
	let y = (y_ + 0.5) * h / sh - 0.5;
	
	let x1 = Math.floor(x);
	let x2 = Math.floor(x + 0.5);
	let y1 = Math.floor(y);
	let y2 = Math.floor(y + 0.5);
	
	x1 = x1 < 0 ? 0 : x1;
	y1 = y1 < 0 ? 0 : y1;
	
	
	x1 = x1 < w - 1 ? x1 : w - 1;
	y1 = y1 < h - 1 ? y1 : h - 1;
	
	x2 = x2 < w - 1 ? x2 : w - 1;
	y2 = y2 < h - 1 ? y2 : h - 1;
	
	// 取出原矩陣中對應四個點的值
	let f11 = data[y1][x1];
	let f21 = data[y1][x2];
	let f12 = data[y2][x1];
	let f22 = data[y2][x2];
	// 計算該點的值
	let xm = x - x1;
	let ym = y - y1;
	let r1 = (1 - xm) * f11 + xm * f21;
	let r2 = (1 - xm) * f12 + xm * f22;
	let value = (1-ym) * r1 + ym * r2;
	
	return value;}/**
 * 雙三次插值法
 * @param sw 目標矩陣的寬度
 * @param sh 目標矩陣的高度
 * @param x_ 目標矩陣中的x坐標
 * @param y_ 目標矩陣中的y坐標
 * @param data 源數據矩陣（二維數組）
 */DataUtil.cubicInterpolation = function (sw, sh, x_, y_, data) {
	let w = data[0].length;
	let h = data.length;
	// 計算縮放后坐標對應源數據上的坐標
	let x = x_ * w / sw;
	let y = y_ * h / sh;
	
	
	// 計算x和y方向的最近的4*4的坐標和權重
	let wcx = DataUtil.getCubicWeight(x);
	let wcy = DataUtil.getCubicWeight(y);
	
	// 權重
	let wx = wcx.weight;
	let wy = wcy.weight;
	
	// 坐標
	let xs = wcx.coordinate;
	let ys = wcy.coordinate;
	
	let val = 0;
	// 遍歷周圍4*4的點，根據權重相加
	for (let j = 0; j < 4; j++) {
		let py = ys[j];
		py = py < 0 ? 0 : py;
		py = py > h - 1 ? h - 1 : py;
		for (let i = 0; i < 4; i++) {
			let px = xs[i];
			px = px < 0 ? 0 : px;
			px = px > w - 1 ? w - 1 : px;
			// 該點的值
			let dv = data[py][px];
			// 該點的權重
			let w_x = wx[i];
			let w_y = wy[j];
			// 根據加權加起來
			val += (dv * w_x * w_y);
		}
	}
	
	return val;}/**
 * 雙三次插值法中，基于BiCubic基函數，計算源坐標v，最近的4*4的坐標和坐標對應的權重
 * @param v 目標矩陣中坐標對應在源矩陣中坐標值
 */DataUtil.getCubicWeight = function (v){
	let a = -0.5;
	
	// 取整
	let nv = Math.floor(v);
	
	// 坐標差值集合
	let xList = new Array(4);
	// 坐標集合
	let xs = new Array(4);
	
	// 最近的4個坐標差值
	xList[0] = nv - v - 1;
	xList[1] = nv - v
	xList[2] = nv - v + 1;
	xList[3] = nv - v + 2;
	// 
	xs[0] = nv - 1;
	xs[1] = nv;
	xs[2] = nv + 1;
	xs[3] = nv + 2;
	
	// 計算權重
	let ws = new Array(4);
	for (let i = 0; i < 4; i++) {
		let val = Math.abs(xList[i]);
		let w = 0;
		// 基于BiCubic基函數的雙三次插值
		if (val <= 1) {
			w = (a + 2) * val * val * val - (a + 3) * val * val + 1;
		} else if (val < 2) {
			w = a * val * val * val - 5 * a * val * val + 8 * a * val - 4 * a;
		}
		ws[i] = w;
	}
	
	return {
		weight: ws,
		coordinate: xs	};}

以上是“如何實現js的雙線性插值和雙三次插值法”這篇文章的所有內容，感謝各位的閱讀！希望分享的內容對大家有幫助，更多相關知識，歡迎關注億速云行業資訊頻道！