您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
JAVA中怎么利用二叉樹對遞歸進行遍歷?相信很多沒有經驗的人對此束手無策,為此本文總結了問題出現的原因和解決方法,通過這篇文章希望你能解決這個問題。
一.基本概念
二叉樹有5種基本形態:
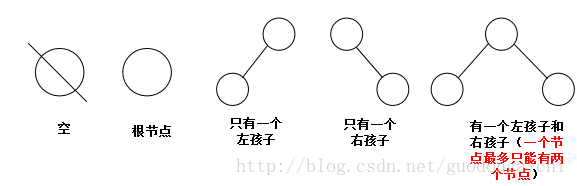
注:二叉樹有序樹,就是說一個節點的左右節點是有大小之分的,我們通常設定為左孩子一定大于右孩子,下面的實現都是基于這個規則的。二叉樹分為三種:滿二叉樹,完全二叉樹,不完全二叉樹
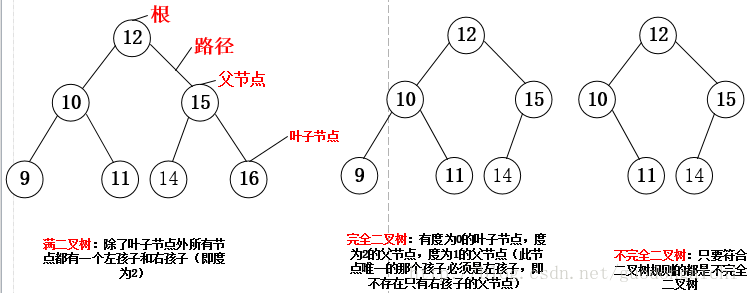
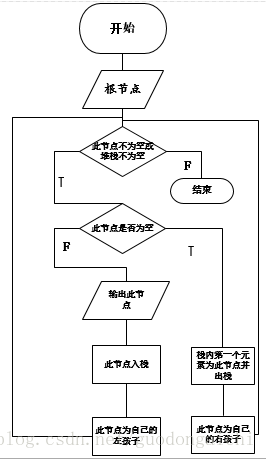
二叉樹的四種遍歷:層次,先序,中序,后序首先是非遞歸實現上圖的滿二叉樹:1.先序:根左右,用棧來實現,下面是它的流程圖和入棧出棧的狀態圖(n是每個節點的值) 輸出:12,10,9,11,15,14,16
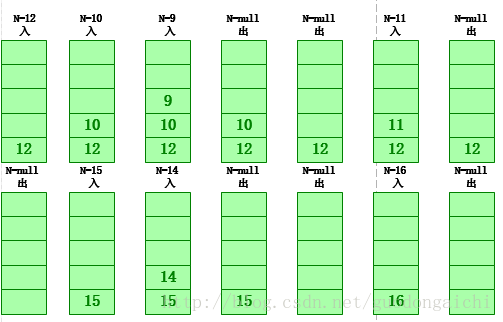
2.中序:左根右,用棧來實現,中序的堆棧狀態和先序一樣,只是輸出的位置不同,先序在入棧前輸出,中序在出棧后輸出 輸出:9,10,11,12,14,15,16
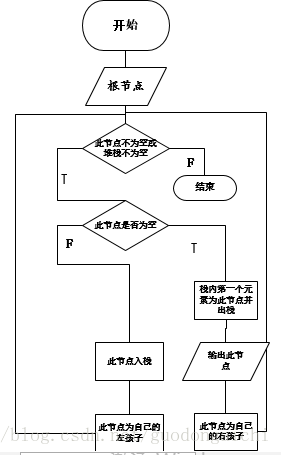
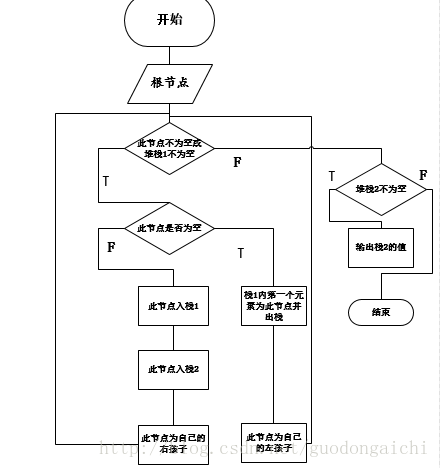
3.后序:左右根,采用了兩個棧 輸出:9,11,10,14,16,15,12
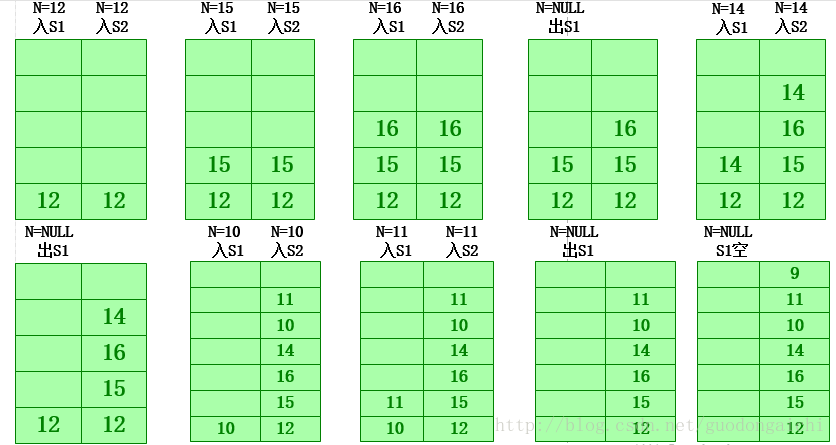
下面是實現的代碼:
//創建一個節點類
class Node {
public int key;//節點的值
public String Data;//節點存儲的內容
public Node leftNode;//左孩子
public Node rightNode;//右孩子
//節點類的構造方法
public Node(int key,String Data){
this.key=key;
this.Data=Data;
this.leftNode=null;
this.rightNode=null;
}
//得到數據
public int getKey(){
return key;
}
}
public class BinaryTree {
public Node root;
public int h=0;
//插入數據
public void insert(int key,String Data){
//實例化一個節點
Node newNode=new Node(key, Data);
//判斷此二叉樹是否有根節點
if(root==null){
root=newNode;
}
else
{
Node current=root;
Node parent;
while(true){
parent=current;
//判斷大小,決定新節點是放在左邊還是右邊
if(key<current.key){
current=current.leftNode;//往左子樹方向找
if(current==null){
parent.leftNode=newNode;//找到葉子節點
return;
}//葉子節點的If end;
}//左子樹的If end;
else{
current=current.rightNode;
if(current==null){
parent.rightNode=newNode;
return;
}//葉子
}//右子樹
}
}
}//insert end;
//打印
public void printlTree(Node node){
System.out.print("*");
System.out.print(node.getKey());
}
//深度
public int Height(Node node){
if(node==null){
return 0;
}
else{
int i=Height(node.leftNode);
int j=Height(node.rightNode);
return (i>j)?(i+1):(j+1);
}
}
//節點個數
public int NodeNum(Node node){
if(node==null){
return 0;
}
return NodeNum(node.leftNode)+NodeNum(node.rightNode)+1;
}
//第K層節點的個數
public int getLeafNodeNum(Node node,int i){
if(node==null){
return 0;
}
else{
if(i==0){
return 1;
}
else{
int numLeft=getLeafNodeNum(node.leftNode,i-1);
int numRight=getLeafNodeNum(node.rightNode,i-1);
return (numLeft+numRight);
}
}
}
//分層遍歷
public void LevelOrder(Node node){
Queue<Node> queue=new LinkedList<Node>();
if(node==null){
return;
}
queue.add(node);
while(!queue.isEmpty()){
Node temp=queue.poll();
System.out.print("*");
System.out.print(temp.getKey());
if(temp.leftNode!=null){
queue.add(temp.leftNode);
}
if(temp.rightNode!=null){
queue.add(temp.rightNode);
}
}
}
//遞歸前序遍歷
public void preOrder(Node node){
if(node!=null){
printlTree(node);
preOrder(node.leftNode);
preOrder(node.rightNode);
}
}
//非遞歸前序遍歷
public void NpreOrder(Node node){
Stack<Node> sk=new Stack<Node>();
Node n=node;
while(!sk.isEmpty()||n!=null){
if(n!=null){
System.out.print("<<<");
System.out.print(n.getKey());
sk.push(n);
n=n.leftNode;
}
else{
n=sk.pop();;
n=n.rightNode;
}
}
}
//中序遍歷
public void inOrder(Node node){
if(node!=null){
preOrder(node.leftNode);
printlTree(node);
preOrder(node.rightNode);
}
}
//非遞歸的中序遍歷
public void NinOrder(Node node){
Stack<Node> s=new Stack<Node>();
Node n=node;
while(n!=null||!s.isEmpty()){
if(n!=null){
s.push(n);
n=n.leftNode;
}
else{
n=s.pop();
System.out.println(n.getKey());
n=n.rightNode;
}
}
}
//后序遍歷
public void postOrder(Node node){
if(node!=null){
preOrder(node.leftNode);
preOrder(node.rightNode);
printlTree(node);
}
}
//非遞歸后序遍歷
public void NpostOrder(Node node){
Stack<Node> s1=new Stack<Node>();//第一次入棧
Stack<Node> s2=new Stack<Node>();//第二次入棧
Node n=node;
while(!s1.isEmpty()||n!=null){
if(n!=null){
s1.push(n);
s2.push(n);
n=n.rightNode;
}
else{
n=s1.pop();
n=n.leftNode;
}
}
while(!s2.isEmpty()){
System.out.println("((("+s2.pop().getKey());
}
}
public static void main(String[] args) {
BinaryTree bt=new BinaryTree();
bt.insert(12, "A");
bt.insert(10, "B");
bt.insert(15, "C");
bt.insert(9, "D");
bt.insert(11, "E");
bt.insert(14, "F");
bt.insert(16, "G");
System.out.println("這個二叉樹的深度:"+bt.Height(bt.root));
System.out.println("這個二叉樹的節點個數:"+bt.NodeNum(bt.root));
System.out.println("前序遍歷:");
bt.preOrder(bt.root);
System.out.println();
System.out.println("非遞歸前序遍歷:");
bt.NpreOrder(bt.root);
System.out.println();
System.out.println("中序遍歷:");
bt.inOrder(bt.root);
System.out.println();
System.out.println("非遞歸中序遍歷:");
bt.NinOrder(bt.root);
System.out.println();
System.out.println("后序遍歷:");
bt.postOrder(bt.root);
System.out.println();
System.out.println("非遞歸后序遍歷:");
bt.NpostOrder(bt.root);
System.out.println();
System.out.println("分層遍歷:");
bt.LevelOrder(bt.root);
System.out.println();
System.out.println("第二層有"+bt.getLeafNodeNum(bt.root, 2));
}
}看完上述內容,你們掌握JAVA中怎么利用二叉樹對遞歸進行遍歷的方法了嗎?如果還想學到更多技能或想了解更多相關內容,歡迎關注億速云行業資訊頻道,感謝各位的閱讀!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。