溫馨提示×
您好，登錄后才能下訂單哦！
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好，登錄后才能下訂單哦！
這期內容當中小編將會給大家帶來有關使用python實現計算圓周率π的方法，文章內容豐富且以專業的角度為大家分析和敘述，閱讀完這篇文章希望大家可以有所收獲。
1.拉馬努金公式：
2.高斯-勒讓德公式：
3.波爾文四次迭代式
這個公式由喬納森·波爾文和彼得·波爾文于1985年發表的。
bailey-borwein-plouffe算法
這個公式簡稱BBP公式，由David Bailey, Peter Borwein和Simon Plouffe于1995年共同發表。它打破了傳統的圓周率的算法，可以計算圓周率的任意第n位，而不用計算前面的n-1位。這為圓周率的分布式計算提供了可行性。
4.丘德諾夫斯基公式
這是由丘德諾夫斯基兄弟發現的，十分適合計算機編程，是目前計算機使用較快的一個公式。
5.萊布尼茨公式
π/4=1-1/3+1/5-1/7+1/9-1/11+……
6.蒙特卡羅法（打鳥法）
一個正方形內部相切一個圓，圓和正方形的面積之比是π/4。
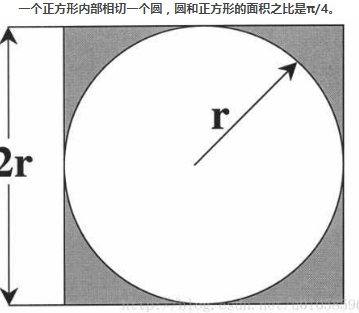
在這個正方形內部，隨機產生n個點（這些點服從均勻分布），計算它們與中心點的距離是否大于圓的半徑，以此判斷是否落在圓的內部。
統計圓內的點數，與n的比值乘以4，就是π的值。理論上，n越大，計算的π值越準。
代碼如下：
import mathimport timescale=10print("執行開始")t=time.process_time()for i in range(scale+1): a,b='**'*i,'..'*(scale-i) c=(i/scale)*100 π=4*(4*math.atan(1/5)-math.atan(1/239)) print("[{}{}->%{}]".format(a,b,c)) time.sleep(0.1)print(π)print("程序用時：{:.2f}s".format(t))print("執行結束")上述就是小編為大家分享的使用python實現計算圓周率π的方法了，如果剛好有類似的疑惑，不妨參照上述分析進行理解。如果想知道更多相關知識，歡迎關注億速云行業資訊頻道。
免責聲明：本站發布的內容（圖片、視頻和文字）以原創、轉載和分享為主，文章觀點不代表本網站立場，如果涉及侵權請聯系站長郵箱：is@yisu.com進行舉報，并提供相關證據，一經查實，將立刻刪除涉嫌侵權內容。
