c語言中常見數據結構是什么

c語言中常見數據結構是什么？這個問題可能是我們日常學習或工作經常見到的。希望通過這個問題能讓你收獲頗深。下面是小編給大家帶來的參考內容，讓我們一起來看看吧！

c語言中，數據結構是指相互之間存在一種或多種特定關系的數據元素的集合，它是計算機存儲、組織數據的方式；常見數據結構有：線性數據結構（數組、鏈表、棧、隊列和線性表）、樹形結構（二叉樹、完全二叉樹、二叉查找樹、堆）、圖形結構（有向圖和無向圖）。

教程

什么是數據結構呢？

數據結構是計算機存儲、組織數據的方式。數據結構是指相互之間存在一種或多種特定關系的數據元素的集合

大部分數據結構的實現都需要借助C語言中的指針和結構體類型

下面，進入今天的重點啦O(∩_∩)O幾種常見的數據結構

（1）線性數據結構：元素之間一般存在元素之間存在一對一關系，是最常用的一類數據結構，典型的有：數組、棧、隊列和線性表

（2）樹形結構：結點間具有層次關系，每一層的一個結點能且只能和上一層的一個結點相關，但同時可以和下一層的多個結點相關，稱為“一對多”關系，常見類型有：樹、堆

（3）圖形結構：在圖形結構中，允許多個結點之間相關，稱為“多對多”關系

下面分別對這幾種數據結構做一個簡單介紹：

1、線性數據結構：典型的有：數組、棧、隊列和線性表

（1）數組和鏈表

a、數組：存放著一組相同類型的數據，需要預先指定數組的長度，有一維數組、二維數組、多維數組等

b、鏈表：鏈表是C語言中一種應用廣泛的結構，它采用動態分配內存的形式實現，用一組任意的存儲單元存放數據元素鏈表的，一般為每個元素增設指針域，用來指向后繼元素

c、數組和鏈表的區別：

從邏輯結構來看：數組必須事先定義固定的長度，不能適應數據動態地增減的情況；鏈表動態地進行存儲分配，可以適應數據動態地增減的情況，且可以方便地插入、刪除數據項（數組中插入、刪除數據項時，需要移動其它數據項）

從內存存儲來看：（靜態)數組從棧中分配空間（用NEW創建的在堆中）, 對于程序員方便快速,但是自由度小；鏈表從堆中分配空間, 自由度大但是申請管理比較麻煩

從訪問方式來看：數組在內存中是連續存儲的，因此，可以利用下標索引進行隨機訪問；鏈表是鏈式存儲結構，在訪問元素的時候只能通過線性的方式由前到后順序訪問，所以訪問效率比數組要低

（2）棧、隊列和線性表：可采用順序存儲和鏈式存儲的方法進行存儲

順序存儲：借助數據元素在存儲空間中的相對位置來表示元素之間的邏輯關系

鏈式存儲：借助表示數據元素存儲地址的指針表示元素之間的邏輯關系

a、棧：只允許在序列末端進行操作，棧的操作只能在棧頂進行，一般棧又被稱為后進先出或先進后出的線性結構

順序棧：采用順序存儲結構的棧稱為順序棧，即需要用一片地址連續的空間來存儲棧的元素，順序棧的類型定義如下：

鏈棧：采用鏈式存儲結構的棧稱為鏈棧：

b、隊列：只允許在序列兩端進行操作，一般隊列也被稱為先進先出的線性結構
循環隊列：采用順序存儲結構的隊列，需要按隊列可能的最大長度分配存儲空空，其類型定義如下：

鏈隊列：采用鏈式存儲結構的隊列稱為鏈隊列，一般需要設置頭尾指針只是鏈表的頭尾結點：

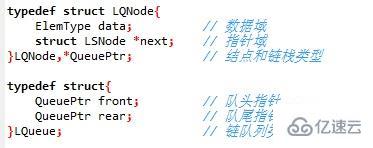
c、線性表：允許在序列任意位置進行操作，線性表的操作位置不受限制，線性表的操作十分靈活，常用操作包括在任意位置插入和刪除，以及查詢和修改任意位置的元素

順序表：采用順序存儲結構表示的線性表稱為順序表，用一組地址連續的存儲單元一次存放線性表的數據元素，即以存儲位置相鄰表示位序相繼的兩個元素之間的前驅和后繼關系，為了避免移動元素，一般在順序表的接口定義中只考慮在表尾插入和刪除元素，如此實現的順序表也可稱為棧表：

線性表：一般包括單鏈表、雙向鏈表、循環鏈表和雙向循環鏈表

單鏈表：

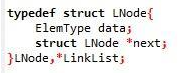
雙向鏈表：

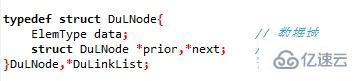
線性表兩種存儲結構的比較：

順序表：

　優點：在順序表中，邏輯中相鄰的兩個元素在物理位置上也相鄰，查找比較方便，存取任一元素的時間復雜度都為O(1)

　缺點：不適合在任意位置插入、刪除元素，因為需要移動元素，平均時間復雜度為O(n)

鏈表：

　優點：在鏈接的任意位置插入或刪除元素只需修改相應指針，不需要移動元素；按需動態分配，不需要按最大需求預先分配一塊連續空空

　缺點：查找不方便，查找某一元素需要從頭指針出發沿指針域查找，因此平均時間復雜度為O(n)

2、樹形結構：結點間具有層次關系，每一層的一個結點能且只能和上一層的一個結點相關，但同時可以和下一層的多個結點相關，稱為“一對多”關系，常見類型有：樹、堆

（1）二叉樹：二叉樹是一種遞歸數據結構，是含有n(n>=0)個結點的有限集合，二叉樹具有以下特點：

二叉樹可以是空樹；二叉樹的每個結點都恰好有兩棵子樹，其中一個或兩個可能為空；二叉樹中每個結點的左、右子樹的位置不能顛倒，若改變兩者的位置，就成為另一棵二叉樹

（2）完全二叉樹：從根起，自上而下，自左而右，給滿二叉樹的每個結點從1到n連續編號，如果每個結點都與深度為k的滿二叉樹中編號從1至n的結點一一對應，則稱為完全二叉樹

a、采用順序存儲結構：用一維數組存儲完全二叉樹，結點的編號對于與結點的下標（如根為1，則根的左孩子為2i=21=2，右孩子為2i+1=21+1=2）

b、采用鏈式存儲結構：

二叉鏈表：

三叉鏈表：它的結點比二叉鏈表多一個指針域parent，用于執行結點的雙親，便于查找雙親結點

兩種存儲結構比較：對于完全二叉樹，采用順序存儲結構既能節省空間，又可利用數組元素的下標值確定結點在二叉樹中的位置及結點之間的關系，但采用順序存儲結構存儲一般二叉樹容易造成空間浪費，鏈式結構可以克服這個缺點

（3）二叉查找樹：二叉查找樹又稱二叉排序樹，或者是一課空二叉樹，或者是具有如下特征的二叉樹：

a、若它的左子樹不空，則左子樹上所有結點的值均小于根結點的值

b、若它的右子樹不空，則右子樹上所有結點的值均大于根結點的值

c、它的左、右子樹也分別是二叉查找樹

（4）平衡二叉樹：平衡二叉查找樹簡稱平衡二叉樹，平衡二叉樹或者是棵空樹，或者是具有下列性質的二叉查找樹：它的左子樹和右子樹都是平衡二叉樹，且左子樹和右子樹的高度之差的絕對值不超過1

平衡二叉樹的失衡及調整主要可歸納為下列四種情況：LL型、RR型、LR型、RL型

（5）樹：樹是含有n(n>=0)個結點的有限集合，在任意一棵非空樹種： a、有且僅有一個特定的稱為根的結點

b、當n>1時，其余結點可分為m(m>0)個互不相交的有限集T1,T2,…,Tm，其中每一個集合本身又是一棵樹，并且T1,T2,…,Tm稱為根的子樹

（6）堆：堆是具有以下特性的完全二叉樹，其所有非葉子結點均不大于（或不小于）其左右孩子結點。若堆中所有非葉子結點均不大于其左右孩子結點，則稱為小頂堆（小根堆），若堆中所有非葉子結點均不小于其左右孩子結點，則稱為大頂堆（大根堆）

（7）并查集：并查集是指由一組不相交子集所構成的集合，記作：S={S1,S2,S3,…,Sn}

（8）B樹

3、圖形結構：在圖形結構中，允許多個結點之間相關，稱為“多對多”關系，可分為有向圖和無向圖

感謝各位的閱讀！看完上述內容，你們對c語言中常見數據結構是什么大概了解了嗎？希望文章內容對大家有所幫助。如果想了解更多相關文章內容，歡迎關注億速云行業資訊頻道。