Python中實現共軛梯度法的案例

小編給大家分享一下Python中實現共軛梯度法的案例，相信大部分人都還不怎么了解，因此分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后大有收獲，下面讓我們一起去了解一下吧！

共軛梯度法是介于最速下降法與牛頓法之間的一個方法，它僅需利用一階導數信息，但克服了最速下降法收斂慢的缺點，又避免了牛頓法需要存儲和計算Hesse矩陣并求逆的缺點，共軛梯度法不僅是解決大型線性方程組最有用的方法之一，也是解大型非線性最優化最有效的算法之一。 在各種優化算法中，共軛梯度法是非常重要的一種。其優點是所需存儲量小，具有步收斂性，穩定性高，而且不需要任何外來參數。

算法步驟：

import random
import numpy as np
import matplotlib.pyplot as plt
 
def goldsteinsearch(f,df,d,x,alpham,rho,t):
 '''
 線性搜索子函數
 數f，導數df，當前迭代點x和當前搜索方向d，t試探系數>1，
 '''
 flag = 0
 
 a = 0
 b = alpham
 fk = f(x)
 gk = df(x)
 
 phi0 = fk
 dphi0 = np.dot(gk, d)
 alpha=b*random.uniform(0,1)
 
 while(flag==0):
  newfk = f(x + alpha * d)
  phi = newfk
  # print(phi,phi0,rho,alpha ,dphi0)
  if (phi - phi0 )<= (rho * alpha * dphi0):
   if (phi - phi0) >= ((1 - rho) * alpha * dphi0):
    flag = 1
   else:
    a = alpha
    b = b
    if (b < alpham):
     alpha = (a + b) / 2
    else:
     alpha = t * alpha
  else:
   a = a
   b = alpha
   alpha = (a + b) / 2
 return alpha
 
 
def Wolfesearch(f,df,d,x,alpham,rho,t):
 '''
 線性搜索子函數
 數f，導數df，當前迭代點x和當前搜索方向d
 σ∈(ρ,1)=0.75
 '''
 sigma=0.75
 
 flag = 0
 
 a = 0
 b = alpham
 fk = f(x)
 gk = df(x)
 
 phi0 = fk
 dphi0 = np.dot(gk, d)
 alpha=b*random.uniform(0,1)
 
 while(flag==0):
  newfk = f(x + alpha * d)
  phi = newfk
  # print(phi,phi0,rho,alpha ,dphi0)
  if (phi - phi0 )<= (rho * alpha * dphi0):
   # if abs(np.dot(df(x + alpha * d),d))<=-sigma*dphi0:
   if (phi - phi0) >= ((1 - rho) * alpha * dphi0):
    flag = 1
   else:
    a = alpha
    b = b
    if (b < alpham):
     alpha = (a + b) / 2
    else:
     alpha = t * alpha
  else:
   a = a
   b = alpha
   alpha = (a + b) / 2
 return alpha
 
def frcg(fun,gfun,x0):
 
 
 # x0是初始點，fun和gfun分別是目標函數和梯度
 # x,val分別是近似最優點和最優值，k是迭代次數
 # dk是搜索方向，gk是梯度方向
 # epsilon是預設精度，np.linalg.norm(gk)求取向量的二范數
 maxk = 5000
 rho = 0.6
 sigma = 0.4
 k = 0
 epsilon = 1e-5
 n = np.shape(x0)[0]
 itern = 0
 W = np.zeros((2, 20000))
 
 f = open("共軛.txt", 'w')
 
 while k < maxk:
   W[:, k] = x0
   gk = gfun(x0)
   itern += 1
   itern %= n
   if itern == 1:
    dk = -gk
   else:
    beta = 1.0 * np.dot(gk, gk) / np.dot(g0, g0)
    dk = -gk + beta * d0
    gd = np.dot(gk, dk)
    if gd >= 0.0:
     dk = -gk
   if np.linalg.norm(gk) < epsilon:
    break
 
   alpha=goldsteinsearch(fun,gfun,dk,x0,1,0.1,2)
   # alpha=Wolfesearch(fun,gfun,dk,x0,1,0.1,2)
   x0+=alpha*dk
 
   f.write(str(k)+' '+str(np.linalg.norm(gk))+"\n")
   print(k,alpha)
   g0 = gk
   d0 = dk
   k += 1
 
 W = W[:, 0:k+1] # 記錄迭代點
 return [x0, fun(x0), k,W]
 
def fun(x):
 return 100 * (x[1] - x[0] ** 2) ** 2 + (1 - x[0]) ** 2
def gfun(x):
 return np.array([-400 * x[0] * (x[1] - x[0] ** 2) - 2 * (1 - x[0]), 200 * (x[1] - x[0] ** 2)])
 
 
if __name__=="__main__":
 X1 = np.arange(-1.5, 1.5 + 0.05, 0.05)
 X2 = np.arange(-3.5, 4 + 0.05, 0.05)
 [x1, x2] = np.meshgrid(X1, X2)
 f = 100 * (x2 - x1 ** 2) ** 2 + (1 - x1) ** 2 # 給定的函數
 plt.contour(x1, x2, f, 20) # 畫出函數的20條輪廓線
 
 x0 = np.array([-1.2, 1])
 x=frcg(fun,gfun,x0)
 print(x[0],x[2])
 # [1.00318532 1.00639618]
 W=x[3]
 # print(W[:, :])
 plt.plot(W[0, :], W[1, :], 'g*-') # 畫出迭代點收斂的軌跡
 plt.show()

代碼中求最優步長用得是goldsteinsearch方法，另外的Wolfesearch是試驗的部分，在本段程序中不起作用。

迭代軌跡：

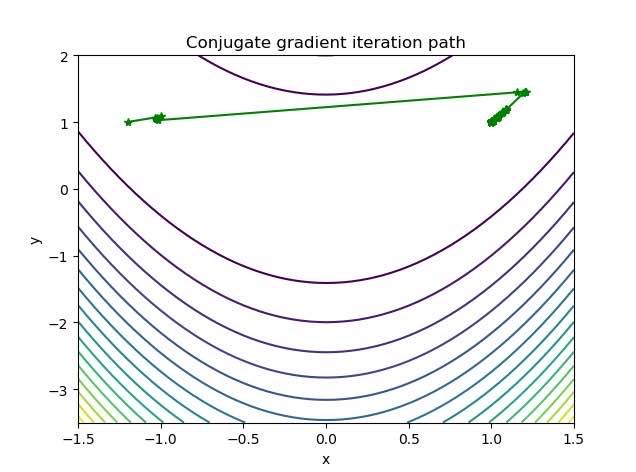
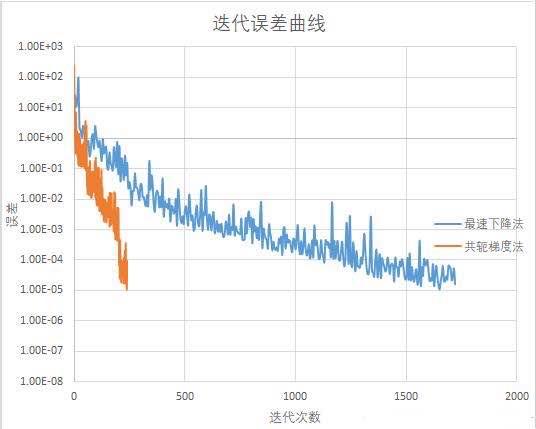
三種最優化方法的迭代次數對比：

以上是Python中實現共軛梯度法的案例的所有內容，感謝各位的閱讀！相信大家都有了一定的了解，希望分享的內容對大家有所幫助，如果還想學習更多知識，歡迎關注億速云行業資訊頻道！