您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這期內容當中小編將會給大家帶來有關一文帶你了解tensorflow之過擬合問題,文章內容豐富且以專業的角度為大家分析和敘述,閱讀完這篇文章希望大家可以有所收獲。
1.構建數據集
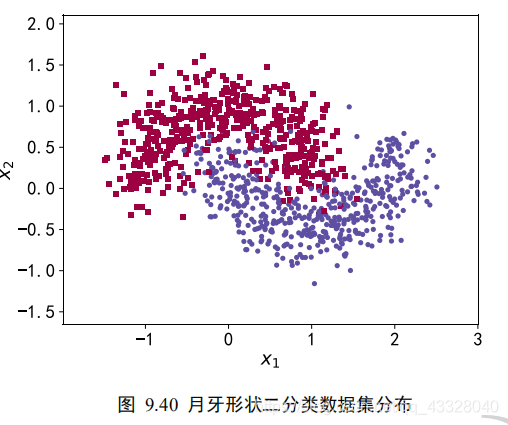
我們使用的數據集樣本特性向量長度為 2,標簽為 0 或 1,分別代表了 2 種類別。借助于 scikit-learn 庫中提供的 make_moons 工具我們可以生成任意多數據的訓練集。
import matplotlib.pyplot as plt # 導入數據集生成工具 import numpy as np import seaborn as sns from sklearn.datasets import make_moons from sklearn.model_selection import train_test_split from tensorflow.keras import layers, Sequential, regularizers from mpl_toolkits.mplot3d import Axes3D
為了演示過擬合現象,我們只采樣了 1000 個樣本數據,同時添加標準差為 0.25 的高斯噪聲數據:
def load_dataset(): # 采樣點數 N_SAMPLES = 1000 # 測試數量比率 TEST_SIZE = None # 從 moon 分布中隨機采樣 1000 個點,并切分為訓練集-測試集 X, y = make_moons(n_samples=N_SAMPLES, noise=0.25, random_state=100) X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=TEST_SIZE, random_state=42) return X, y, X_train, X_test, y_train, y_test
make_plot 函數可以方便地根據樣本的坐標 X 和樣本的標簽 y 繪制出數據的分布圖:
def make_plot(X, y, plot_name, file_name, XX=None, YY=None, preds=None, dark=False, output_dir=OUTPUT_DIR):
# 繪制數據集的分布, X 為 2D 坐標, y 為數據點的標簽
if dark:
plt.style.use('dark_background')
else:
sns.set_style("whitegrid")
axes = plt.gca()
axes.set_xlim([-2, 3])
axes.set_ylim([-1.5, 2])
axes.set(xlabel="$x_1$", ylabel="$x_2$")
plt.title(plot_name, fontsize=20, fontproperties='SimHei')
plt.subplots_adjust(left=0.20)
plt.subplots_adjust(right=0.80)
if XX is not None and YY is not None and preds is not None:
plt.contourf(XX, YY, preds.reshape(XX.shape), 25, alpha=0.08, cmap=plt.cm.Spectral)
plt.contour(XX, YY, preds.reshape(XX.shape), levels=[.5], cmap="Greys", vmin=0, vmax=.6)
# 繪制散點圖,根據標簽區分顏色m=markers
markers = ['o' if i == 1 else 's' for i in y.ravel()]
mscatter(X[:, 0], X[:, 1], c=y.ravel(), s=20, cmap=plt.cm.Spectral, edgecolors='none', m=markers, ax=axes)
# 保存矢量圖
plt.savefig(output_dir + '/' + file_name)
plt.close()def mscatter(x, y, ax=None, m=None, **kw):
import matplotlib.markers as mmarkers
if not ax: ax = plt.gca()
sc = ax.scatter(x, y, **kw)
if (m is not None) and (len(m) == len(x)):
paths = []
for marker in m:
if isinstance(marker, mmarkers.MarkerStyle):
marker_obj = marker
else:
marker_obj = mmarkers.MarkerStyle(marker)
path = marker_obj.get_path().transformed(
marker_obj.get_transform())
paths.append(path)
sc.set_paths(paths)
return scX, y, X_train, X_test, y_train, y_test = load_dataset() make_plot(X,y,"haha",'月牙形狀二分類數據集分布.svg')
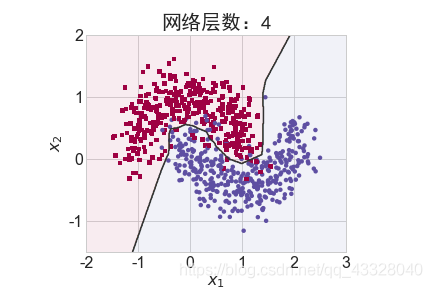
2.網絡層數的影響
為了探討不同的網絡深度下的過擬合程度,我們共進行了 5 次訓練實驗。在𝑛 ∈ [0,4]時,構建網絡層數為n + 2層的全連接層網絡,并通過 Adam 優化器訓練 500 個 Epoch
def network_layers_influence(X_train, y_train):
# 構建 5 種不同層數的網絡
for n in range(5):
# 創建容器
model = Sequential()
# 創建第一層
model.add(layers.Dense(8, input_dim=2, activation='relu'))
# 添加 n 層,共 n+2 層
for _ in range(n):
model.add(layers.Dense(32, activation='relu'))
# 創建最末層
model.add(layers.Dense(1, activation='sigmoid'))
# 模型裝配與訓練
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X_train, y_train, epochs=N_EPOCHS, verbose=1)
# 繪制不同層數的網絡決策邊界曲線
# 可視化的 x 坐標范圍為[-2, 3]
xx = np.arange(-2, 3, 0.01)
# 可視化的 y 坐標范圍為[-1.5, 2]
yy = np.arange(-1.5, 2, 0.01)
# 生成 x-y 平面采樣網格點,方便可視化
XX, YY = np.meshgrid(xx, yy)
preds = model.predict_classes(np.c_[XX.ravel(), YY.ravel()])
print(preds)
title = "網絡層數:{0}".format(2 + n)
file = "網絡容量_%i.png" % (2 + n)
make_plot(X_train, y_train, title, file, XX, YY, preds, output_dir=OUTPUT_DIR + '/network_layers')

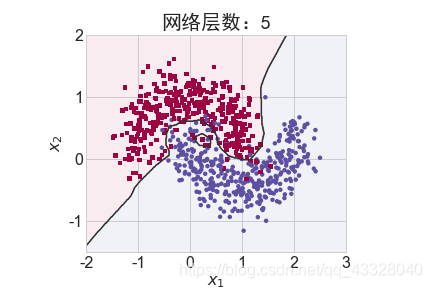
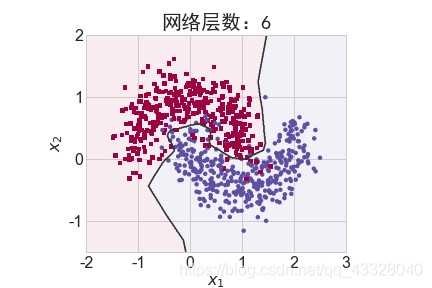
3.Dropout的影響
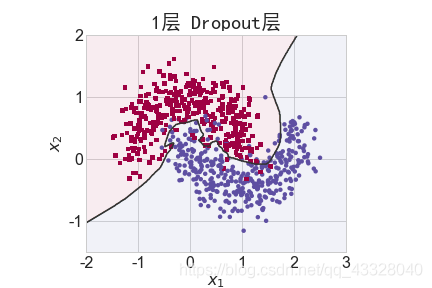
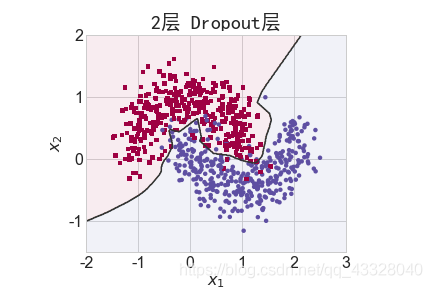
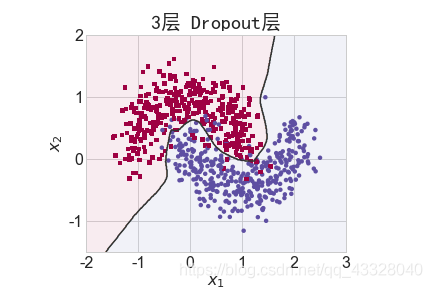
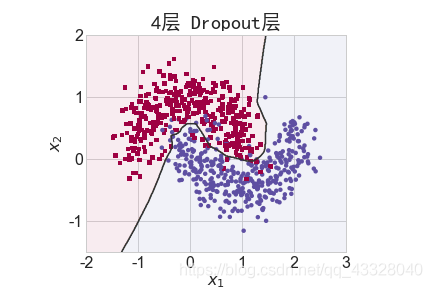
為了探討 Dropout 層對網絡訓練的影響,我們共進行了 5 次實驗,每次實驗使用 7 層的全連接層網絡進行訓練,但是在全連接層中間隔插入 0~4 個 Dropout 層并通過 Adam優化器訓練 500 個 Epoch
def dropout_influence(X_train, y_train):
# 構建 5 種不同數量 Dropout 層的網絡
for n in range(5):
# 創建容器
model = Sequential()
# 創建第一層
model.add(layers.Dense(8, input_dim=2, activation='relu'))
counter = 0
# 網絡層數固定為 5
for _ in range(5):
model.add(layers.Dense(64, activation='relu'))
# 添加 n 個 Dropout 層
if counter < n:
counter += 1
model.add(layers.Dropout(rate=0.5))
# 輸出層
model.add(layers.Dense(1, activation='sigmoid'))
# 模型裝配
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# 訓練
model.fit(X_train, y_train, epochs=N_EPOCHS, verbose=1)
# 繪制不同 Dropout 層數的決策邊界曲線
# 可視化的 x 坐標范圍為[-2, 3]
xx = np.arange(-2, 3, 0.01)
# 可視化的 y 坐標范圍為[-1.5, 2]
yy = np.arange(-1.5, 2, 0.01)
# 生成 x-y 平面采樣網格點,方便可視化
XX, YY = np.meshgrid(xx, yy)
preds = model.predict_classes(np.c_[XX.ravel(), YY.ravel()])
title = "無Dropout層" if n == 0 else "{0}層 Dropout層".format(n)
file = "Dropout_%i.png" % n
make_plot(X_train, y_train, title, file, XX, YY, preds, output_dir=OUTPUT_DIR + '/dropout')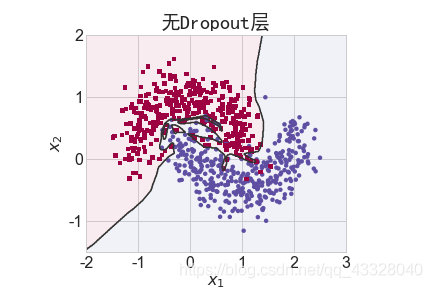
4.正則化的影響
為了探討正則化系數𝜆對網絡模型訓練的影響,我們采用 L2 正則化方式,構建了 5 層的神經網絡,其中第 2,3,4 層神經網絡層的權值張量 W 均添加 L2 正則化約束項:
def build_model_with_regularization(_lambda): # 創建帶正則化項的神經網絡 model = Sequential() model.add(layers.Dense(8, input_dim=2, activation='relu')) # 不帶正則化項 # 2-4層均是帶 L2 正則化項 model.add(layers.Dense(256, activation='relu', kernel_regularizer=regularizers.l2(_lambda))) model.add(layers.Dense(256, activation='relu', kernel_regularizer=regularizers.l2(_lambda))) model.add(layers.Dense(256, activation='relu', kernel_regularizer=regularizers.l2(_lambda))) # 輸出層 model.add(layers.Dense(1, activation='sigmoid')) model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy']) # 模型裝配 return model
下面我們首先來實現一個權重可視化的函數
def plot_weights_matrix(model, layer_index, plot_name, file_name, output_dir=OUTPUT_DIR):
# 繪制權值范圍函數
# 提取指定層的權值矩陣
weights = model.layers[layer_index].get_weights()[0]
shape = weights.shape
# 生成和權值矩陣等大小的網格坐標
X = np.array(range(shape[1]))
Y = np.array(range(shape[0]))
X, Y = np.meshgrid(X, Y)
# 繪制3D圖
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.xaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.yaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
ax.zaxis.set_pane_color((1.0, 1.0, 1.0, 0.0))
plt.title(plot_name, fontsize=20, fontproperties='SimHei')
# 繪制權值矩陣范圍
ax.plot_surface(X, Y, weights, cmap=plt.get_cmap('rainbow'), linewidth=0)
# 設置坐標軸名
ax.set_xlabel('網格x坐標', fontsize=16, rotation=0, fontproperties='SimHei')
ax.set_ylabel('網格y坐標', fontsize=16, rotation=0, fontproperties='SimHei')
ax.set_zlabel('權值', fontsize=16, rotation=90, fontproperties='SimHei')
# 保存矩陣范圍圖
plt.savefig(output_dir + "/" + file_name + ".svg")
plt.close(fig)在保持網絡結構不變的條件下,我們通過調節正則化系數 𝜆 = 0.00001,0.001,0.1,0.12,0.13 來測試網絡的訓練效果,并繪制出學習模型在訓練集上的決策邊界曲線
def regularizers_influence(X_train, y_train):
for _lambda in [1e-5, 1e-3, 1e-1, 0.12, 0.13]: # 設置不同的正則化系數
# 創建帶正則化項的模型
model = build_model_with_regularization(_lambda)
# 模型訓練
model.fit(X_train, y_train, epochs=N_EPOCHS, verbose=1)
# 繪制權值范圍
layer_index = 2
plot_title = "正則化系數:{}".format(_lambda)
file_name = "正則化網絡權值_" + str(_lambda)
# 繪制網絡權值范圍圖
plot_weights_matrix(model, layer_index, plot_title, file_name, output_dir=OUTPUT_DIR + '/regularizers')
# 繪制不同正則化系數的決策邊界線
# 可視化的 x 坐標范圍為[-2, 3]
xx = np.arange(-2, 3, 0.01)
# 可視化的 y 坐標范圍為[-1.5, 2]
yy = np.arange(-1.5, 2, 0.01)
# 生成 x-y 平面采樣網格點,方便可視化
XX, YY = np.meshgrid(xx, yy)
preds = model.predict_classes(np.c_[XX.ravel(), YY.ravel()])
title = "正則化系數:{}".format(_lambda)
file = "正則化_%g.svg" % _lambda
make_plot(X_train, y_train, title, file, XX, YY, preds, output_dir=OUTPUT_DIR + '/regularizers')regularizers_influence(X_train, y_train)
上述就是小編為大家分享的一文帶你了解tensorflow之過擬合問題了,如果剛好有類似的疑惑,不妨參照上述分析進行理解。如果想知道更多相關知識,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。