您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家介紹python中怎么推導線性回歸模型,內容非常詳細,感興趣的小伙伴們可以參考借鑒,希望對大家能有所幫助。
首先,先看一張圖:
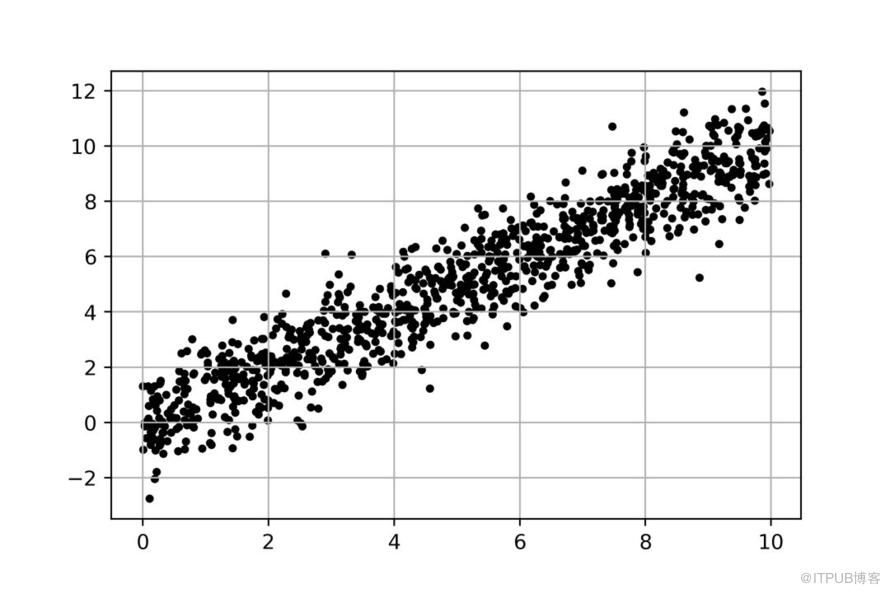
圖是我們在初中學習過的直角坐標系二維平面,上面遍布著一些點。從整體趨勢看,y隨x的增大而增大。如果曾經你和我一樣,數學每次考試都是90的話,那么接下來,我相信你會情不自禁地做一件事:
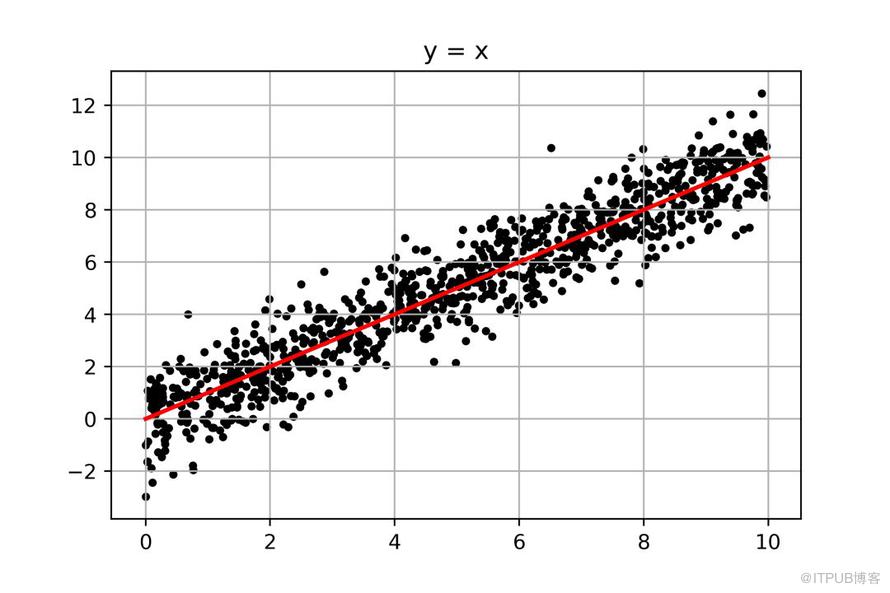
沒錯,我們會以(0,0)和(10,10)為兩點,畫出一條貫穿其中的線,從視覺上,這條紅線正好把所有點一分為二,其對應的數學表達式為:
y=x
而這就是我們線性回歸所要做的事:找到一組數學表達式(圖中的紅線),用來反映數據(圖中的點)的變化規律。
目標有了,問題也來了:
貫穿圖中密密麻麻點的線有無數條,為什么不是y=2x,y=x+1,偏偏是y=x呢?
我們又是通過何種方法去找到這條線呢?
先解決第一個問題,上天書:
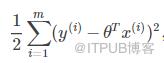
這個式子就是第一個問題的解,沒見過的符號太多,看不懂是吧?那么我來翻譯一下:
先求出(每個點的Y值-以每個點的X值通過函數求出的Y值)的平方
求和;
乘以1/2
再通俗點:
把每個點的實際y值與它通過某個函數求出的y值的差的平方加起來,再乘以1/2。
而文章開篇中的均方差損失,MSE,平方損失函數,二次代價函數其實都指的是它。這個式子其實計算的是真實值和用函數預測的值之間的誤差之和。那么第一個問題就迎刃而解了:哪一個表達式所求出的誤差和最小,就是我們要找的那條“紅線”。
我們繼續解決第二個問題,先上圖:
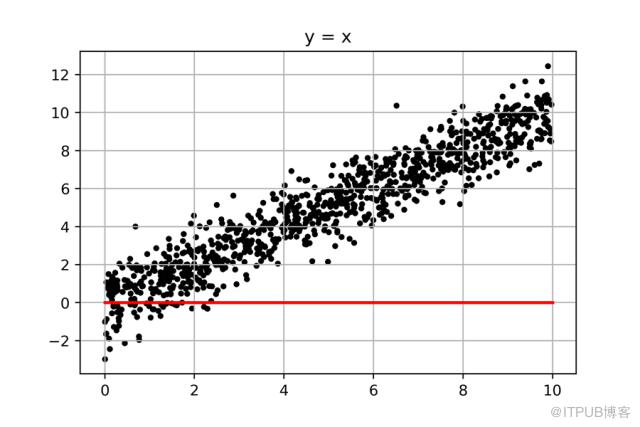
這個問題還要簡單,我們只要從斜率為0的那條“紅線”(y=0*X)開始畫線,然后一點點增大斜率,每條線求一個誤差值,找出其中誤差值最小的那條線,就大功告成了。而中間有著巨大計算量的遍歷過程,我們可以通過python,瞬間完成。
————————
線性回歸的Python實現
————————
重點:梯度下降法!
導入一些包,待用:
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import MinMaxScaler
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_context('notebook')
sns.set_style('white')
導入案例數據:
model_data = pd.read_csv('model_data.csv',engine='python')
model_data.head()
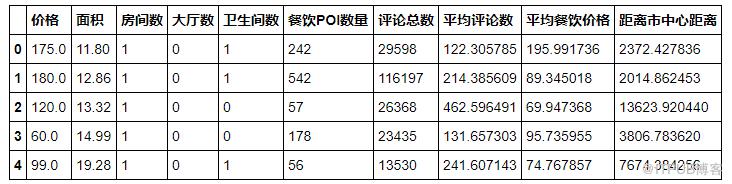
數據是一份上海的房價數據,我們要把房屋價格作為因變量y,房屋面積,房間數附近餐飲POI數量,評論,距離市中心距離等作為自變量,擬合一個線性回歸模型,用于預測房價。
根據要求提取自變量和因變量:
feat_cols = model_data.columns.tolist()[1:]
print(feat_cols)
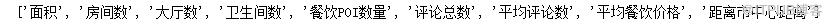
X = model_data[feat_cols].values
y = model_data['價格'].values
構建損失函數:
def Cost_Function(X,y,theta):
'''
需要傳入的參數為
X:自變量
y:應變量
theta:權重
使用均方誤差(MSE),作為損失函數
'''
m = y.size #求出y的個數(一共多少條數據)
t = X.dot(theta) #權重和變量點乘,計算出使用當前權重時的預測值
c = 0 #定義損失值
c = 1/(2*m) * (np.sum(np.square(t-y)))
#預測值與實際值的差值,平方后除以數據的條數,計算出均方誤差。最后乘以1/2(無實際意義,方便以后計算)
return c #返回損失值
*θ為每個變量前的權重,什么是權重?比如y=2x,2就是自變量x的權重
求損失值我們就用先前說到的損失函數。如果你夠仔細,可能會有一個問題,我們的損失函數前需要乘以一個1/2,似乎沒有特別的意義。恭喜你很機智,1/2的確沒有任何意義,只是為了接下來方便求導。
構建梯度下降法:
def GradientDescent(X, y, feat_cols, alpha=0.3, num_iters=10000):
'''
需傳入參數為
X:自變量
y:應變量
feat_cols:變量列表
alpha:學習率,默認0.3
num_iters:迭代次數,默認10000次
使用梯度下降法迭代權重
'''
scaler = MinMaxScaler() #最大最小值歸一化自變量
X = scaler.fit_transform(X) #歸一化
m = y.size #求出y的個數(一共多少條數據)
J_history = np.zeros(num_iters) #創建容納每次迭代后損失值得矩陣,初始值為0
theta = np.zeros(len(feat_cols)+1) #設置默認權重,0
for iter in np.arange(num_iters): #根據迭代次數,開始迭代
t = X.dot(theta) #權重和變量點乘,計算出使用當前權重時的預測值
theta = theta - alpha*(1/m)*(X.T.dot(t-y))
#對代價函數求導,算出下降最快的方向,乘以學習率(下降的速度),再用原來的權重相減,得到新的權重
J_history[iter] = Cost_Function(X, y, theta) #求出新的權重時的損失值,存入矩陣
return(theta, J_history) #返回最終的權重和歷次迭代的損失值
這是構造模型最為核心的部分。我們不斷迭代,尋找最優的那條“紅線”的過程,其實是在不斷調整每個自變量的權重。而每個權重每次到底怎么調整,增大還是減小(方向),這就需要我們對損失函數求導。
如果數學不好,不理解,我們用圖來說明一下:
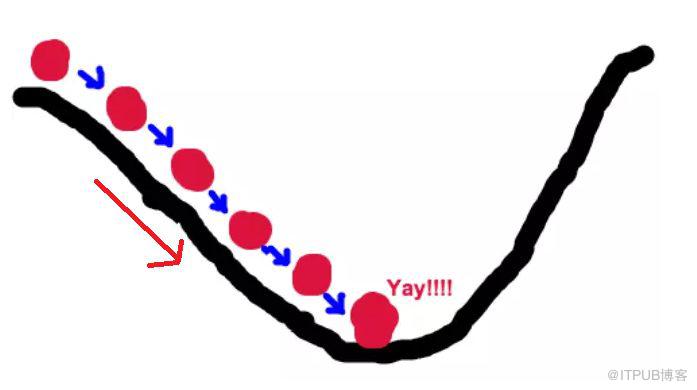
好比,我們站在懸崖頂端,要找到最快能達到懸崖底部的方向,那么顯而易見,你所在位置最陡峭的方向,就是正確的方向,而求導就是找到最陡峭的方向(切線斜率絕對值最大的點)。
山坡是凹凸不平的,所以我們每走一步都需要重新尋找方向,這就是迭代的過程;其次,每次的步子也不能跨太大,萬一跨錯地方了,不好糾正,所以我們又需要設置一個步子的大小——學習率。
所以梯度下降法的公式就是:
每一次更新的權重= 前一次的權重-學習率*損失函數的導數。
在理解了下山這個場景以后,我們就能順利的完成梯度下降法的構建,并且通過python函數求出最后每個變量的權重和每次迭代過后的損失值。
構建繪制損失值變化圖的函數:
def plot_Cost(GD_result):
'''
繪制權重變化情況
需傳入參數為
GD_result:梯度下降法結果
'''
theta , Cost = GD_result #得到權重和損失值
print('theta: ',theta.ravel()) #打印權重
plt.plot(Cost) #繪制損失值變化情況
plt.title('COST change')
plt.ylabel('Cost')
plt.xlabel('Iterations')
plt.grid()
plt.show()
這個很簡單,就是通過前面梯度下降法求得的歷次迭代后的損失值,畫出變化曲線。
最后把所有函數匯總,就是我們的線性回歸模型了:
def lr_function(X,y,feat_cols):
'''
需要輸入的變量為
X:自變量
y:應變量
feat_cols:變量列表
'''
def score(y_p,y):
'''
y_p:預測值
y:真實值
dimension:樣本數量
計算R^和調整R^
'''
aa=y_p.copy(); bb=y.copy()
if len(aa)!=len(bb):
print('not same length')
return np.nan
cc=aa-bb
wcpfh=sum(cc**2) #誤差平方和
# RR means R_Square
RR=1-sum((bb-aa)**2)/sum((bb-np.mean(bb))**2)
return RR#返回R^
X = np.c_[np.ones(X.shape[0]),X]
GD_result = GradientDescent(X, y, feat_cols)
plot_Cost(GD_result)
y_p = np.dot(X,GD_result[0])
RR = score(y_p,y)
return RR,y_p,GD_result[0] #返回R^,預測值
一般對于每個機器學習模型,都需要有一個指標衡量其擬合程度,而線性模型我們使用的是我們所熟知的可決系數R^2。為了求出R^2,我在函數中又套用了一個簡單的求解函數,具體過程不贅述了,通讀代碼就能明白。通常R^2越接近1,表示模型擬合程度越好。
模型封裝完畢,下面是見證奇跡的時刻!
model_result = lr_function(X,y,feat_cols)
print('R^2為:{}'.format(round(model_result[0],4)))
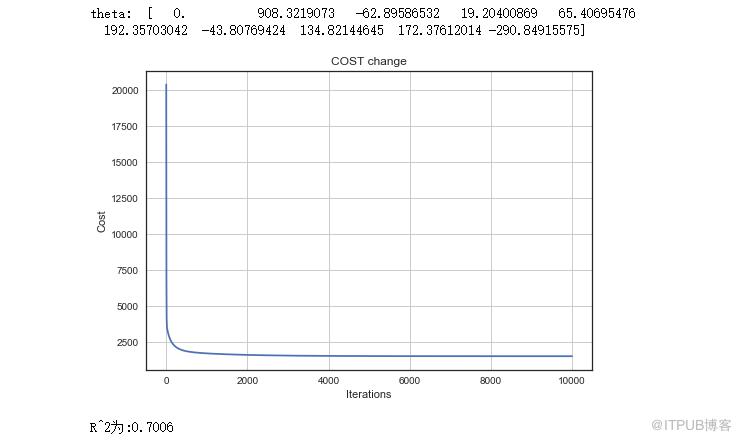
通過模型,我們求出了每個自變量的權重,圖表反應了損失值由大變小的過程,在10000次迭代的過程中,一開始速度很快,越到后面越趨于平緩。
最后是R^2為0.70,有70%的擬合度,尚可。
————————
線性回歸模型的驗證
————————
為了驗證我們自己編寫的模型是否準確,我們也可以使用python機器學習工具包sklearn,對同樣的數據,用線性回歸模型擬合,查看最后的R^2是否一致。
先對變量標準化:
scaler = MinMaxScaler()
X = scaler.fit_transform(X)
使用LinearRegression()進行擬合,并求出R^2:
lr = LinearRegression()
lr.fit(X,y)
R2 = lr.score(X,y)
print('R^2為:{}'.format(round(R2,4)))
R^2同樣為0.7,代表我們自己編寫的模型沒有問題。
最后,我們繪制一張真實值與預測值對比圖,可視化模型結果:
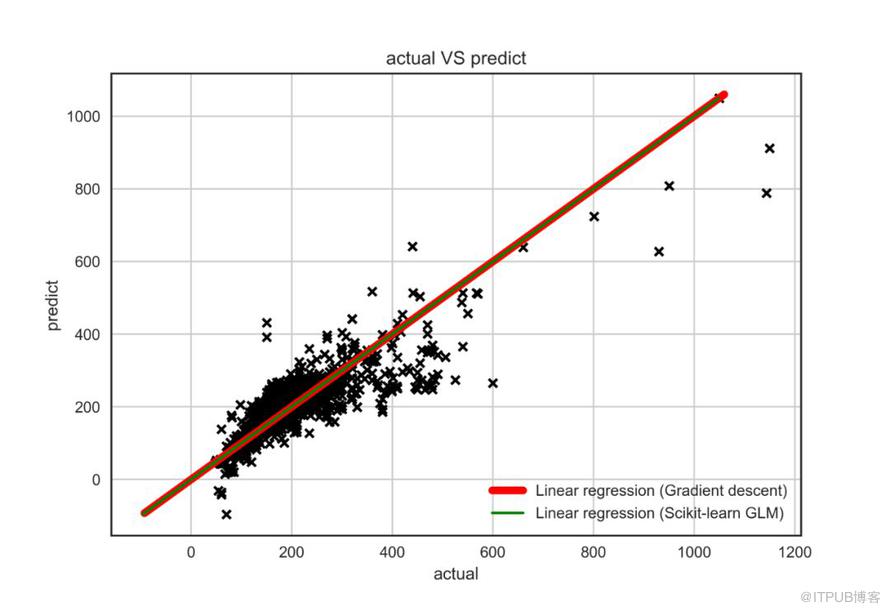
關于python中怎么推導線性回歸模型就分享到這里了,希望以上內容可以對大家有一定的幫助,可以學到更多知識。如果覺得文章不錯,可以把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。