您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
牛頓法、梯度下降法、最小二乘法的原理以及利用它們解決實際問題的python編程
一、牛頓法原理
1、產生背景

2、牛頓迭代公式
二、梯度下降法原理
根據計算梯度時所用數據量不同,可以分為三種基本方法:批量梯度下降法(Batch Gradient Descent, BGD)、小批量梯度下降法(Mini-batch Gradient Descent, MBGD)以及隨機梯度下降法(Stochastic Gradient Descent, SGD)。
梯度下降法的一般求解框架
三、最小二乘法原理
最小二乘法(又稱最小平方法)是一種數學優化技術。它通過最小化誤差的平方和尋找數據的最佳函數匹配。利用最小二乘法可以簡便地求得未知的數據,并使得這些求得的數據與實際數據之間誤差的平方和為最小。最小二乘法還可用于曲線擬合。其他一些優化問題也可通過最小化能量或最大化熵用最小二乘法來表達。
詳細原理請參考:https://baike.baidu.com/item/%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98%E6%B3%95/2522346#4
四、運用梯度下降法原理解決實際問題的python編程舉例
1、問題如下
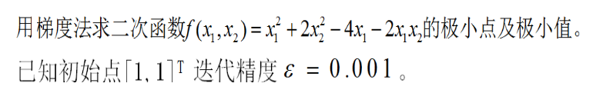
2、導入所需要的包
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
from mpl_toolkits.mplot3d import Axes3D
import warnings
3、畫出函數圖像
def f2(x1,x2):
return x1 ** 2 + 2 * x2 ** 2 -4*x1- 2 * x1*x2
X1 = np.arange(-4,4,0.2)
X2 = np.arange(-4,4,0.2)
X1, X2 = np.meshgrid(X1, X2) # 生成xv、yv,將X1、X2變成n*m的矩陣,方便后面繪圖
Y = np.array(list(map(lambda t : f2(t[0],t[1]),zip(X1.flatten(),X2.flatten()))))
Y.shape = X1.shape # 1600的Y圖還原成原來的(40,40)
%matplotlib inline
#作圖
fig = plt.figure(facecolor='w')
ax = Axes3D(fig)
ax.plot_surface(X1,X2,Y,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.set_title(u'$ x1 ** 2 + 2 * x2 ** 2 -4*x1- 2 * x1*x2 $')
plt.show()
4、求極小點和極值點
# 解決中文顯示問題
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
%matplotlib inline
# 二維原始圖像
def f2(x, y):
return x ** 2 + 2 * y ** 2 -4*x- 2 * x*y
## 偏函數
def hx1(x, y):
return 2*x-4-2*y
def hx2(x, y):
return 4*y-2*x
x1 = 4
x2 = 4
alpha = 0.001
#保存梯度下降經過的點
GD_X1 = [x1]
GD_X2 = [x2]
GD_Y = [f2(x1,x2)]
# 定義y的變化量和迭代次數
y_change = f2(x1,x2)
iter_num = 0
while(iter_num < 10000) :
tmp_x1 = x1 - alpha * hx1(x1,x2)
tmp_x2 = x2 - alpha * hx2(x1,x2)
tmp_y = f2(tmp_x1,tmp_x2)
f_change = np.absolute(tmp_y - f2(x1,x2))
x1 = tmp_x1
x2 = tmp_x2
GD_X1.append(x1)
GD_X2.append(x2)
GD_Y.append(tmp_y)
iter_num += 1
print(u"最終結果為:(%.5f, %.5f, %.5f)" % (x1, x2, f2(x1,x2)))
print(u"迭代過程中X的取值,迭代次數:%d" % iter_num)
print(GD_X1)
# 作圖
fig = plt.figure(facecolor='w',figsize=(20,18))
ax = Axes3D(fig)
ax.plot_surface(X1,X2,Y,rstride=1,cstride=1,cmap=plt.cm.jet)
ax.plot(GD_X1,GD_X2,GD_Y,'ko-')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('z')
ax.set_title(u'函數;\n學習率:%.3f; 最終解:(%.3f, %.3f, %.3f);迭代次數:%d' % (alpha, x1, x2, f2(x1,x2), iter_num))
plt.show()
最終結果為:(4.00043, 2.00027, -8.00000)
迭代過程中X的取值,迭代次數:10000
從上面求出的結果可以得到極小點為(4,2),極小值為-8
5、用Excel求上個函數的極小點和極小值
實驗結果如下圖:
依舊可以清晰地看出該函數的極小點為(4,2),極值點為-8
五、使用梯度下降法和最小二乘法求解多元函數python編程舉例
1、問題如下
用梯度下降法和最小二乘法根據以下圖片的數據進行多元線性回歸并求解相關系數
將數據寫入Excel中
2、使用梯度下降法求解多元函數
代碼如下:
import matplotlib.pyplot as plt
import numpy as np
from numpy import array
import pandas as pd
# 讀取數據文件
df=pd.read_csv("C:/Users/LOL/Desktop/店鋪多元回歸.csv")
%matplotlib notebook
df=df.values
x_data=df[:,:2]
y_data=df[:,2]
#定義學習率、斜率、截據
#設方程為y=theta1*x1+theta2*x2+theta0
lr=0.00001
theta0=0
theta1=0
theta2=0
#定義最大迭代次數
epochs=10000
#定義最小二乘法函數-損失函數(代價函數)
def compute_error(theta0,theta1,theta2,x_data,y_data):
totalerror=0
for i in range(0,len(x_data)):#定義一共有多少樣本點
totalerror=totalerror+(y_data[i]-(theta1*x_data[i,0]+theta2*x_data[i,1]+theta0))**2
return totalerror/float(len(x_data))/2
#梯度下降算法求解參數
def gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs):
m=len(x_data)
for i in range(epochs):
theta0_grad=0
theta1_grad=0
theta2_grad=0
for j in range(0,m):
theta0_grad-=(1/m)*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta2)+y_data[j])
theta1_grad-=(1/m)*x_data[j,0]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
theta2_grad-=(1/m)*x_data[j,1]*(-(theta1*x_data[j,0]+theta2*x_data[j,1]+theta0)+y_data[j])
theta0=theta0-lr*theta0_grad
theta1=theta1-lr*theta1_grad
theta2=theta2-lr*theta2_grad
return theta0,theta1,theta2
#進行迭代求解 鄭州婦科醫院 http://www.120zzkd.com/
theta0,theta1,theta2=gradient_descent_runner(x_data,y_data,theta0,theta1,theta2,lr,epochs)
print('迭代次數:{0} 學習率:{1}之后 a0={2},a1={3},a2={4},代價函數為{5}'.format(epochs,lr,theta0,theta1,theta2,compute_error(theta0,theta1,theta2,x_data,y_data)))
print("多元線性回歸方程為:y=",theta1,"X1+",theta2,"X2+",theta0)
迭代次數:10000 學習率:1e-05之后 a0=5.3774162274868,a1=45.0533119768975,a2=-0.19626929358281256,代價函數為366.7314528822914
多元線性回歸方程為:y= 45.0533119768975 X1+ -0.19626929358281256 X2+ 5.3774162274868
3、用最小二乘法求解
代碼如下:
import numpy as np
import pandas as pd
#變量初始化
X=[]
Y=[]
B=[]
Q_e=0
Q_E=0
#從csv文件中讀取數據
def get_data(file_name):
data=pd.read_csv(file_name,header=0)
data=np.array(data)
Y=data[:,data.shape[1]-1]#預測對象位于最后一列
X=data[:,0:data.shape[1]-1]
print(X.shape)
return X,Y
return X,Y
X,Y=get_data('C:/Users/LOL/Desktop/店鋪多元回歸.csv')
X=np.mat(np.c_[np.ones(X.shape[0]),X])#為系數矩陣增加常數項系數
Y=np.mat(Y)#數組轉化為矩陣
B=np.linalg.inv(X.T*X)*(X.T)*(Y.T)
print("第一項為常數項,其他為回歸系數",B)#輸出系數,第一項為常數項,其他為回歸系數
print("輸入店鋪面積,距離最近的車站距離,預測營業額:",np.mat([1,10,80])*B ,"萬日元")#預測結果
#相關系數
Y_mean=np.mean(Y)
for i in range(Y.size):
Q_e+=pow(np.array((Y.T)[i]-X[i]*B),2)
Q_E+=pow(np.array(X[i]*B)-Y_mean,2)
R2=Q_E/(Q_e+Q_E)
print("R2的值:",R2)
(10, 2)
第一項為常數項,其他為回歸系數 [[65.32391639]
[41.51347826]
[-0.34088269]]
輸入店鋪面積,距離最近的車站距離,預測營業額: [[453.1880841]] 萬日元
R2的值: [[0.94523585]]
4、使用Excel求解
由上面三種方法求到的結果對比,可以清晰地看出用最小二乘法和Excel求出的結果一致,而用梯度下降法求解有一定的誤差
六、總結
最小二乘法:能通過最小化誤差的平方和尋找數據的最佳函數匹配,但是使用有一定局限性,在回歸過程中,回歸的關聯式不可能全部通過每個回歸數據點。
梯度下降法:是通過梯度方向和步長,直接求解目標函數的最小值時的參數,越接近最優值時,步長應該不斷減小,否則會在最優值附近來回震蕩。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。