有哪些基于Python的經典排序算法

有哪些基于Python的經典排序算法？針對這個問題，這篇文章詳細介紹了相對應的分析和解答，希望可以幫助更多想解決這個問題的小伙伴找到更簡單易行的方法。

一、排序的基本概念和分類

所謂排序，就是使一串記錄，按照其中的某個或某些關鍵字的大小，遞增或遞減的排列起來的操作。排序算法，就是如何使得記錄按照要求排列的方法。

排序的穩定性：
經過某種排序后，如果兩個記錄序號同等，且兩者在原無序記錄中的先后秩序依然保持不變，則稱所使用的排序方法是穩定的，反之是不穩定的。

內排序和外排序
內排序：排序過程中，待排序的所有記錄全部放在內存中
外排序：排序過程中，使用到了外部存儲。
通常討論的都是內排序。

影響內排序算法性能的三個因素：

時間復雜度：即時間性能，高效率的排序算法應該是具有盡可能少的關鍵字比較次數和記錄的移動次數空間復雜度：主要是執行算法所需要的輔助空間，越少越好。算法復雜性。主要是指代碼的復雜性。

根據排序過程中借助的主要操作，可把內排序分為：

插入排序交換排序選擇排序歸并排序

按照算法復雜度可分為兩類：

簡單算法：包括冒泡排序、簡單選擇排序和直接插入排序改進算法：包括希爾排序、堆排序、歸并排序和快速排序

以下的七種排序算法只是所有排序算法中最經典的幾種，不代表全部。

二、 冒泡排序

冒泡排序（Bubble sort）：時間復雜度O(n^2)
交換排序的一種。其核心思想是：兩兩比較相鄰記錄的關鍵字，如果反序則交換，直到沒有反序記錄為止。

其實現細節可以不同，比如下面3種：

最簡單排序實現:bubble_sort_simple

冒泡排序:bubble_sort

改進的冒泡排序:bubble_sort_advance

#!/usr/bin/env python# -*- coding:utf-8 -*-# Author: Liu Jiang# Python 3.5# 冒泡排序算法class SQList:
    def __init__(self, lis=None):
        self.r = lis    def swap(self, i, j):
        """定義一個交換元素的方法，方便后面調用。"""
        temp = self.r[i]
        self.r[i] = self.r[j]
        self.r[j] = temp    def bubble_sort_simple(self):
        """
        最簡單的交換排序，時間復雜度O(n^2)
        """
        lis = self.r
        length = len(self.r)        for i in range(length):            for j in range(i+1, length):                if lis[i] > lis[j]:
                    self.swap(i, j)    def bubble_sort(self):
        """
        冒泡排序，時間復雜度O(n^2)
        """
        lis = self.r
        length = len(self.r)        for i in range(length):
            j = length-2
            while j >= i:                if lis[j] > lis[j+1]:
                    self.swap(j, j+1)
                j -= 1

    def bubble_sort_advance(self):
        """
        冒泡排序改進算法，時間復雜度O(n^2)
        設置flag，當一輪比較中未發生交換動作，則說明后面的元素其實已經有序排列了。
        對于比較規整的元素集合，可提高一定的排序效率。
        """
        lis = self.r
        length = len(self.r)
        flag = True
        i = 0
        while i < length and flag:
            flag = False
            j = length - 2
            while j >= i:                if lis[j] > lis[j + 1]:
                    self.swap(j, j + 1)
                    flag = True
                j -= 1
            i += 1

    def __str__(self):
        ret = ""
        for i in self.r:
            ret += " %s" % i        return retif __name__ == '__main__':
    sqlist = SQList([4,1,7,3,8,5,9,2,6])    # sqlist.bubble_sort_simple()
    # sqlist.bubble_sort()
    sqlist.bubble_sort_advance()
    print(sqlist)

簡單選擇排序（simple selection sort）:時間復雜度O(n^2)
通過n-i次關鍵字之間的比較，從n-i+1個記錄中選出關鍵字最小的記錄，并和第i（1<=i<=n)個記錄進行交換。

通俗的說就是，對尚未完成排序的所有元素，從頭到尾比一遍，記錄下最小的那個元素的下標，也就是該元素的位置。再把該元素交換到當前遍歷的最前面。其效率之處在于，每一輪中比較了很多次，但只交換一次。因此雖然它的時間復雜度也是O(n^2)，但比冒泡算法還是要好一點。

#!/usr/bin/env python# -*- coding:utf-8 -*-# Author: Liu Jiang# Python 3.5# 簡單選擇排序class SQList:
    def __init__(self, lis=None):
        self.r = lis    def swap(self, i, j):
        """定義一個交換元素的方法，方便后面調用。"""
        temp = self.r[i]
        self.r[i] = self.r[j]
        self.r[j] = temp    def select_sort(self):
        """
        簡單選擇排序，時間復雜度O(n^2)
        """
        lis = self.r
        length = len(self.r)        for i in range(length):
            minimum = i            for j in range(i+1, length):                if lis[minimum] > lis[j]:
                    minimum = j            if i != minimum:
                self.swap(i, minimum)    def __str__(self):
        ret = ""
        for i in self.r:
            ret += " %s" % i        return retif __name__ == '__main__':
    sqlist = SQList([4, 1, 7, 3, 8, 5, 9, 2, 6, 0])
    sqlist.select_sort()
    print(sqlist)

四、直接插入排序

直接插入排序（Straight Insertion Sort）:時間復雜度O(n^2)
基本操作是將一個記錄插入到已經排好序的有序表中，從而得到一個新的、記錄數增1的有序表。

#!/usr/bin/env python# -*- coding:utf-8 -*-# Author: Liu Jiang# Python 3.5# 直接插入排序class SQList:
    def __init__(self, lis=None):
        self.r = lis    def insert_sort(self):
        lis = self.r
        length = len(self.r)        # 下標從1開始
        for i in range(1, length):            if lis[i] < lis[i-1]:
                temp = lis[i]
                j = i-1
                while lis[j] > temp and j >= 0:
                    lis[j+1] = lis[j]
                    j -= 1
                lis[j+1] = temp    def __str__(self):
        ret = ""
        for i in self.r:
            ret += " %s" % i        return retif __name__ == '__main__':
    sqlist = SQList([4, 1, 7, 3, 8, 5, 9, 2, 6, 0])
    sqlist.insert_sort()
    print(sqlist)

該算法需要一個記錄的輔助空間。最好情況下，當原始數據就是有序的時候，只需要一輪對比，不需要移動記錄，此時時間復雜度為O(n)。然而，這基本是幻想。

五、希爾排序

希爾排序（Shell Sort）是插入排序的改進版本，其核心思想是將原數據集合分割成若干個子序列，然后再對子序列分別進行直接插入排序，使子序列基本有序，最后再對全體記錄進行一次直接插入排序。

這里最關鍵的是跳躍和分割的策略，也就是我們要怎么分割數據，間隔多大的問題。通常將相距某個“增量”的記錄組成一個子序列，這樣才能保證在子序列內分別進行直接插入排序后得到的結果是基本有序而不是局部有序。下面的例子中通過：increment = int(increment/3)+1來確定“增量”的值。

希爾排序的時間復雜度為：O(n^(3/2))

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author: Liu Jiang
# Python 3.5
# 希爾排序class SQList:
    def __init__(self, lis=None):
        self.r = lis    def shell_sort(self):
        """希爾排序"""
        lis = self.r
        length = len(lis)
        increment = len(lis)        
        while increment > 1:
            increment = int(increment/3)+1
            for i in range(increment+1, length):                
                if lis[i] < lis[i - increment]:
                    temp = lis[i]
                    j = i - increment                    
            while j >= 0 and temp < lis[j]:
                        lis[j+increment] = lis[j]
                        j -= increment
                    lis[j+increment] = temp    
        def __str__(self):
            ret = ""
            for i in self.r:
                ret += " %s" % i        
            return ret
if __name__ == '__main__':
    sqlist = SQList([4, 1, 7, 3, 8, 5, 9, 2, 6, 0,123,22])
    sqlist.shell_sort()
    print(sqlist)

六、堆排序

堆是具有下列性質的完全二叉樹：
每個分支節點的值都大于或等于其左右孩子的值，稱為大頂堆；
每個分支節點的值都小于或等于其做右孩子的值，稱為小頂堆；
因此，其根節點一定是所有節點中最大（最小）的值。

如果按照層序遍歷的方式（廣度優先）給節點從1開始編號，則節點之間滿足如下關系：

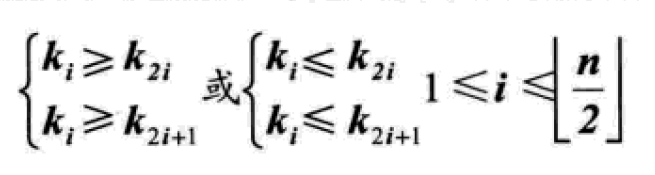
堆排序（Heap Sort）就是利用大頂堆或小頂堆的性質進行排序的方法。堆排序的總體時間復雜度為O(nlogn)。（下面采用大頂堆的方式）

其核心思想是：將待排序的序列構造成一個大頂堆。此時，整個序列的最大值就是堆的根節點。將它與堆數組的末尾元素交換，然后將剩余的n-1個序列重新構造成一個大頂堆。反復執行前面的操作，最后獲得一個有序序列。

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author: Liu Jiang
# Python 3.5
# 堆排序class SQList:
    def __init__(self, lis=None):
        self.r = lis    
        def swap(self, i, j):
        """定義一個交換元素的方法，方便后面調用。"""
        temp = self.r[i]
        self.r[i] = self.r[j]
        self.r[j] = temp    
        def heap_sort(self):
        length = len(self.r)
        i = int(length/2)        # 將原始序列構造成一個大頂堆
        # 遍歷從中間開始，到0結束，其實這些是堆的分支節點。
        while i >= 0:
            self.heap_adjust(i, length-1)
            i -= 1
        # 逆序遍歷整個序列，不斷取出根節點的值，完成實際的排序。
        j = length-1
        while j > 0:            # 將當前根節點，也就是列表最開頭，下標為0的值，交換到最后面j處
            self.swap(0, j)            # 將發生變化的序列重新構造成大頂堆
            self.heap_adjust(0, j-1)
            j -= 1
    def heap_adjust(self, s, m):
        """核心的大頂堆構造方法，維持序列的堆結構。"""
        lis = self.r
        temp = lis[s]
        i = 2*s           
        while i <= m:            
        if i < m and lis[i] < lis[i+1]:
                i += 1
            if temp >= lis[i]:                
                break
            lis[s] = lis[i]
            s = i
            i *= 2
        lis[s] = temp    def __str__(self):
        ret = ""
        for i in self.r:
            ret += " %s" % i        
            return ret
if __name__ == '__main__':
    sqlist = SQList([4, 1, 7, 3, 8, 5, 9, 2, 6, 0, 123, 22])
    sqlist.heap_sort()
    print(sqlist)

堆排序的運行時間主要消耗在初始構建堆和重建堆的反復篩選上。
其初始構建堆時間復雜度為O(n)。
正式排序時，重建堆的時間復雜度為O(nlogn)。
所以堆排序的總體時間復雜度為O(nlogn)。

堆排序對原始記錄的排序狀態不敏感，因此它無論最好、最壞和平均時間復雜度都是O(nlogn)。在性能上要好于冒泡、簡單選擇和直接插入算法。

空間復雜度上，只需要一個用于交換的暫存單元。但是由于記錄的比較和交換是跳躍式的，因此，堆排序也是一種不穩定的排序方法。

此外，由于初始構建堆的比較次數較多，堆排序不適合序列個數較少的排序工作。

七、歸并排序

歸并排序（Merging Sort）：建立在歸并操作上的一種有效的排序算法,該算法是采用分治法（Divide and Conquer）的一個非常典型的應用。將已有序的子序列合并，得到完全有序的序列；即先使每個子序列有序，再使子序列段間有序。若將兩個有序表合并成一個有序表，稱為二路歸并。

#!/usr/bin/env python
# -*- coding:utf-8 -*-
# Author: Liu Jiang
# Python 3.5
# 歸并排序
class SQList:
    def __init__(self, lis=None):
        self.r = lis    
    def swap(self, i, j):
        """定義一個交換元素的方法，方便后面調用。"""
        temp = self.r[i]
        self.r[i] = self.r[j]
        self.r[j] = temp    
     def merge_sort(self):
        self.msort(self.r, self.r, 0, len(self.r)-1)    
     def msort(self, list_sr, list_tr, s, t):
         temp = [None for i in range(0, len(list_sr))]        
        if s == t:
            list_tr[s] = list_sr[s]        
        else:
            m = int((s+t)/2)
            self.msort(list_sr, temp, s,  m)
            self.msort(list_sr, temp, m+1, t)
            self.merge(temp, list_tr, s, m, t)    
     def merge(self, list_sr, list_tr, i, m,  n):
        j = m+1
        k = i        
        while i <= m and j <= n:            
            if list_sr[i] < list_sr[j]:
               list_tr[k] = list_sr[i]
              i += 1
           else:
              list_tr[k] = list_sr[j]
              j += 1
           k += 1
        if i <= m:            
            for l in range(0, m-i+1):
               list_tr[k+l] = list_sr[i+l]        
        if j <= n:            
           for l in range(0, n-j+1):
              list_tr[k+l] = list_sr[j+l]    
    def __str__(self):
        ret = ""
       for i in self.r:
           ret += " %s" % i        
       return ret
if __name__ == '__main__':
    sqlist = SQList([4, 1, 7, 3, 8, 5, 9, 2, 6, 0, 12, 77, 34, 23])
    sqlist.merge_sort()
    print(sqlist)

另外一個版本：

def merge(lfrom, lto, low, mid, high):
    """
    兩段需要歸并的序列從左往右遍歷，逐一比較，小的就放到
    lto里去，lfrom下標+1，lto下標+1，然后再取，再比，再放，
    最后lfrom里的兩段比完了，lto里留下的就是從小到大排好的一段。
    :param lfrom: 原來的列表
    :param lto: 緩存的列表
    :param low: 左邊一段的開頭下標
    :param mid: 左右兩段的中間相隔的下標
    :param high: 右邊一段的最右下標
    :return:
    """
    i, j, k = low, mid, low    
    while i < mid and j < high:        
        if lfrom[i] <= lfrom[j]:
            lto[k] = lfrom[i]
            i += 1
        else:
            lto[k] = lfrom[j]
            j += 1
        k += 1
    while i < mid:
        lto[k] = lfrom[i]
        i += 1
        k += 1
    while j < high:
        lto[k] = lfrom[j]
        j += 1
        k += 1def merge_pass(lfrom, lto, llen, slen):
    """
    用來處理所有需要合并的段，這需要每段的長度，以及列表的總長。
    最后的if語句處理表最后部分不規則的情況。
    :param lfrom: 原來的列表
    :param lto: 緩存的列表
    :param llen: 列表總長
    :param slen: 每段的長度
    :return:
    """
    i = 0
    while i+2*slen < llen:
        merge(lfrom, lto, i, i+slen, i+2*slen)
        i += 2*slen    if i+slen < llen:
        merge(lfrom, lto, i, i+slen, llen)    
            else:        
        for j in range(i, llen):
            lto[j] = lfrom[j]
    def merge_sort(lst):
    """
    主函數。
    先安排一個同樣大小的列表，作為輔助空間。
    然后在兩個列表直接做往復的歸并，每歸并一次slen的長度增加一倍，
    逐漸向llen靠攏，當slen==llen時說明歸并結束了。
    歸并完成后最終結果可能恰好保存在templist里，因此代碼里做兩次歸并，
    保證最后的結果體現在原始的lst列表里。
    :param lst: 要排序的原始列表
    :return:
    """
    slen, llen = 1, len(lst)
    templist = [None]*llen    while slen < llen:
        merge_pass(lst, templist, llen, slen)
        slen *= 2
        merge_pass(templist, lst, llen, slen)
        slen *= 2

歸并排序對原始序列元素分布情況不敏感，其時間復雜度為O(nlogn)。

歸并排序在計算過程中需要使用一定的輔助空間，用于遞歸和存放結果，因此其空間復雜度為O(n+logn)。

歸并排序中不存在跳躍，只有兩兩比較，因此是一種穩定排序。

總之，歸并排序是一種比較占用內存，但效率高，并且穩定的算法。

八、快速排序

快速排序（Quick Sort）由圖靈獎獲得者Tony Hoare發明，被列為20世紀十大算法之一。冒泡排序的升級版，交換排序的一種。快速排序的時間復雜度為O(nlog(n))。

快速排序算法的核心思想：通過一趟排序將待排記錄分割成獨立的兩部分，其中一部分記錄的關鍵字均比另一部分記錄的關鍵字小，然后分別對這兩部分繼續進行排序，以達到整個記錄集合的排序目的。

#!/usr/bin/env python# -*- coding:utf-8 -*-# Author: Liu Jiang# Python 3.5# 快速排序class SQList:
    def __init__(self, lis=None):
        self.r = lis    def swap(self, i, j):
        """定義一個交換元素的方法，方便后面調用。"""
        temp = self.r[i]
        self.r[i] = self.r[j]
        self.r[j] = temp    def quick_sort(self):
        """調用入口"""
        self.qsort(0, len(self.r)-1)    def qsort(self, low, high):
        """遞歸調用"""
        if low < high:
            pivot = self.partition(low, high)
            self.qsort(low, pivot-1)
            self.qsort(pivot+1, high)    def partition(self, low, high):
        """
        快速排序的核心代碼。
        其實就是將選取的pivot_key不斷交換，將比它小的換到左邊，將比它大的換到右邊。
        它自己也在交換中不斷變換自己的位置，直到完成所有的交換為止。
        但在函數調用的過程中，pivot_key的值始終不變。
        :param low:左邊界下標
        :param high:右邊界下標
        :return:分完左右區后pivot_key所在位置的下標
        """
        lis = self.r
        pivot_key = lis[low]        
        while low < high:            
        while low < high and lis[high] >= pivot_key:
                high -= 1
            self.swap(low, high)            
            while low < high and lis[low] <= pivot_key:
                low += 1
            self.swap(low, high)        
            return low    
        def __str__(self):
            ret = ""
        for i in self.r:
           ret += " %s" % i        
        return ret
if __name__ == '__main__':
    sqlist = SQList([4, 1, 7, 3, 8, 5, 9, 2, 6, 0, 123, 22])
    sqlist.quick_sort()
    print(sqlist)

另外一個版本：

def quick_sort(nums):
    # 封裝一層的目的是方便用戶調用
    def qsort(lst, begin, end):
        if begin >= end:            
        return
        i = begin
        key = lst[begin]        
        for j in range(begin+1, end+1):            
        if lst[j] < key:
                i += 1
                lst[i], lst[j] = lst[j], lst[i]
        lst[begin], lst[i] = lst[i], lst[begin]
        qsort(lst, begin, i-1)
        qsort(lst,i+1,end)
    qsort(nums, 0, len(nums)-1)

快速排序的時間性能取決于遞歸的深度。當pivot_key恰好處于記錄關鍵碼的中間值時，大小兩區的劃分比較均衡，接近一個平衡二叉樹，此時的時間復雜度為O(nlog(n))。當原記錄集合是一個正序或逆序的情況下，分區的結果就是一棵斜樹，其深度為n-1，每一次執行大小分區，都要使用n-i次比較，其最終時間復雜度為O(n^2)。在一般情況下，通過數學歸納法可證明，快速排序的時間復雜度為O(nlog(n))。但是由于關鍵字的比較和交換是跳躍式的，因此，快速排序是一種不穩定排序。同時由于采用的遞歸技術，該算法需要一定的輔助空間，其空間復雜度為O(logn)。

下面是一個實例測試數據：

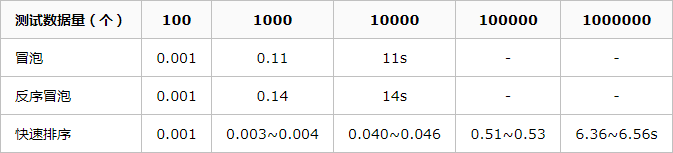
從數據中可見：

數據過萬，冒泡算法基本不可用。測試時間忠實的反映了n平方的時間復雜度，數據擴大10倍，耗時增加100倍對于Python的列表，反序遍歷比正序遍歷還是要消耗一定的時間的快速排序在數據較大時，其威力顯現，但不夠穩定，總體還是維護了nlog(n)的復雜度。

基本的快速排序還有可以優化的地方：

1. 優化選取的pivot_key

前面我們每次選取pivot_key的都是子序列的第一個元素，也就是lis[low]，這就比較看運氣。運氣好時，該值處于整個序列的靠近中間值，則構造的樹比較平衡，運氣比較差，處于最大或最小位置附近則構造的樹接近斜樹。
為了保證pivot_key選取的盡可能適中，采取選取序列左中右三個特殊位置的值中，處于中間值的那個數為pivot_key，通常會比直接用lis[low]要好一點。在代碼中，在原來的pivot_key = lis[low]這一行前面增加下面的代碼：

m = low + int((high-low)/2)if lis[low] > lis[high]:
    self.swap(low, high)if lis[m] > lis[high]:
    self.swap(high, m)if lis[m] > lis[low]:
    self.swap(m, low)

如果覺得這樣還不夠好，還可以將整個序列先劃分為3部分，每一部分求出個pivot_key，再對3個pivot_key再做一次上面的比較得出最終的pivot_key。這時的pivot_key應該很大概率是一個比較靠譜的值。

2. 減少不必要的交換

原來的代碼中pivot_key這個記錄總是再不斷的交換中，其實這是沒必要的，完全可以將它暫存在某個臨時變量中，如下所示：

def partition(self, low, high):
        
        lis = self.r
        m = low + int((high-low)/2)        
        if lis[low] > lis[high]:
            self.swap(low, high)        
            if lis[m] > lis[high]:
            self.swap(high, m)        
            if lis[m] > lis[low]:
            self.swap(m, low)
        pivot_key = lis[low]        # temp暫存pivot_key的值
        temp = pivot_key        
        while low < high:            
        while low < high and lis[high] >= pivot_key:
                high -= 1
            # 直接替換，而不交換了
            lis[low] = lis[high]            
            while low < high and lis[low] <= pivot_key:
                low += 1
            lis[high] = lis[low]
            lis[low] = temp        return low

3. 優化小數組時的排序

快速排序算法的遞歸操作在進行大量數據排序時，其開銷能被接受，速度較快。但進行小數組排序時則不如直接插入排序來得快，也就是殺雞用牛刀，未必就比菜刀來得快。
因此，一種很樸素的做法就是根據數據的多少，做個使用哪種算法的選擇而已，如下改寫qsort方法：

def qsort(self, low, high):
    """根據序列長短，選擇使用快速排序還是簡單插入排序"""
    # 7是一個經驗值，可根據實際情況自行決定該數值。
    MAX_LENGTH = 7
    if high-low < MAX_LENGTH:        
        if low < high:
            pivot = self.partition(low, high)
            self.qsort(low, pivot - 1)
            self.qsort(pivot + 1, high)    
                else:        # insert_sort方法是我們前面寫過的簡單插入排序算法
        self.insert_sort()

4. 優化遞歸操作

可以采用尾遞歸的方式對整個算法的遞歸操作進行優化，改寫qsort方法如下：

def qsort(self, low, high):
    """根據序列長短，選擇使用快速排序還是簡單插入排序"""
    # 7是一個經驗值，可根據實際情況自行決定該數值。
    MAX_LENGTH = 7
    if high-low < MAX_LENGTH:        # 改用while循環
        while low < high:
            pivot = self.partition(low, high)
            self.qsort(low, pivot - 1)            # 采用了尾遞歸的方式
            low = pivot + 1
    else:        # insert_sort方法是我們前面寫過的簡單插入排序算法
        self.insert_sort()

九、排序算法總結

排序算法的分類：

沒有十全十美的算法，有有點就會有缺點，即使是快速排序算法，也只是整體性能上的優越，也存在排序不穩定，需要大量輔助空間，不適于少量數據排序等缺點。

七種排序算法性能對比

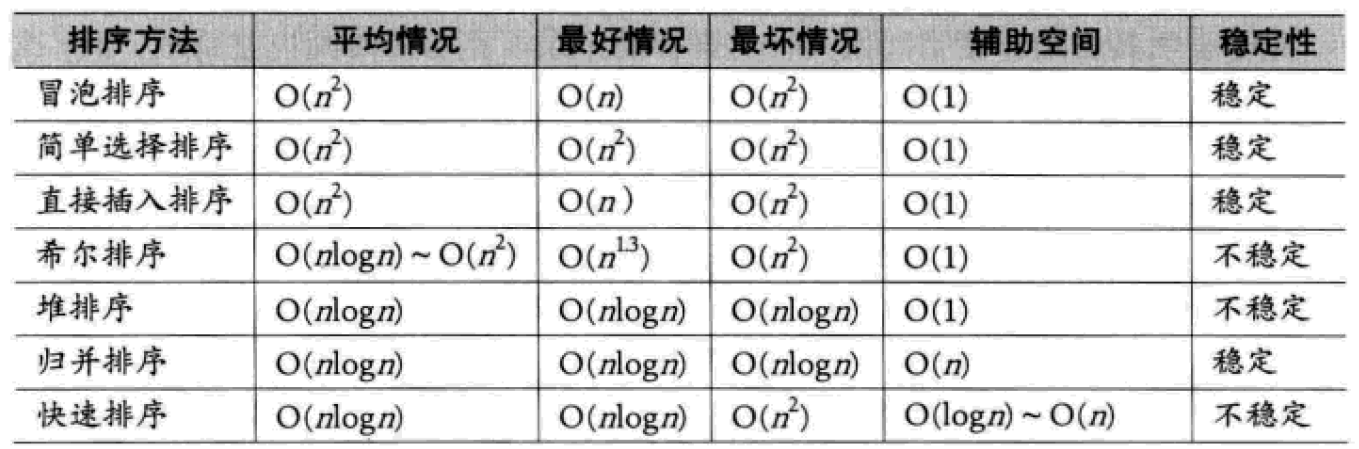
如果待排序列基本有序，請直接使用簡單的算法，不要使用復雜的改進算法。歸并排序和快速排序雖然性能高，但是需要更多的輔助空間。其實就是用空間換時間。待排序列的元素個數越少，就越適合用簡單的排序方法；元素個數越多就越適合用改進的排序算法。簡單選擇排序雖然在時間性能上不好，但它在空間利用上性能很高。特別適合，那些數據量不大，每條數據的信息量又比較多的一類元素的排序。

關于有哪些基于Python的經典排序算法問題的解答就分享到這里了，希望以上內容可以對大家有一定的幫助，如果你還有很多疑惑沒有解開，可以關注億速云行業資訊頻道了解更多相關知識。