您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
首先看兩張路徑壓縮的圖片:
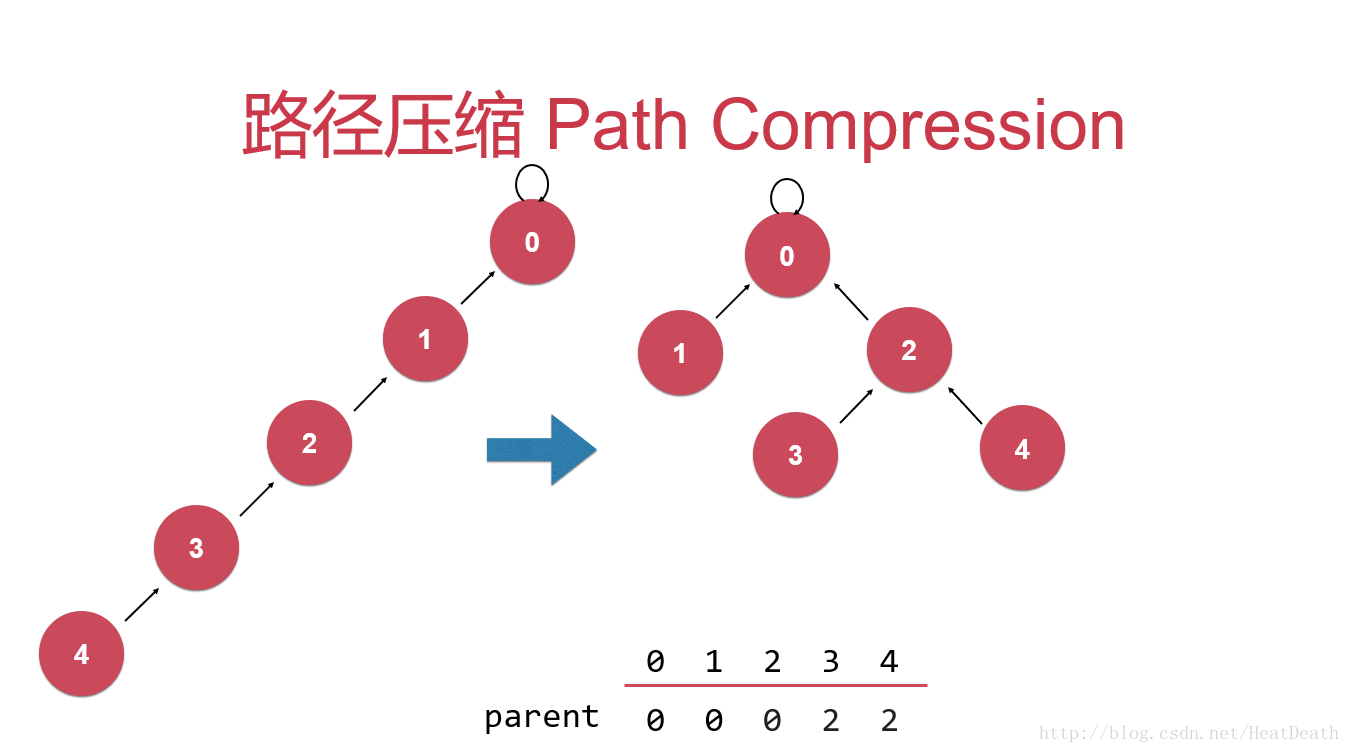
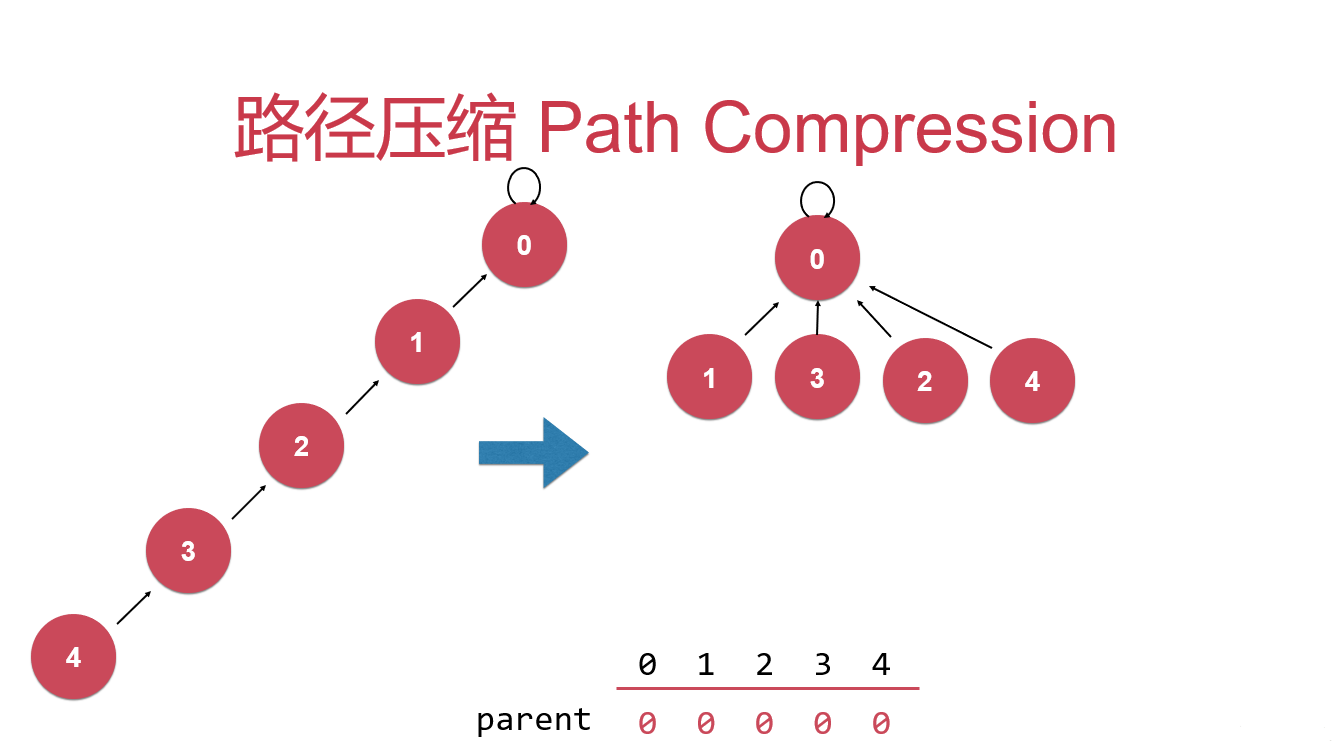
并查集(Union-find Sets)是一種非常精巧而實用的數據結構,它主要用于處理一些不相交集合的合并問題。一些常見的用途有求連通子圖、求最小生成樹的 Kruskal 算法和求最近公共祖先(Least Common Ancestors, LCA)等。
使用并查集時,首先會存在一組不相交的動態集合 S={S 1 ,S 2 ,⋯,S k } ,一般都會使用一個整數表示集合中的一個元素。
每個集合可能包含一個或多個元素,并選出集合中的某個元素作為代表。每個集合中具體包含了哪些元素是不關心的,具體選擇哪個元素作為代表一般也是不關心的。我們關心的是,對于給定的元素,可以很快的找到這個元素所在的集合(的代表),以及合并兩個元素所在的集合,而且這些操作的時間復雜度都是常數級的。
并查集的基本操作有三個:
makeSet(s):建立一個新的并查集,其中包含 s 個單元素集合。
unionSet(x, y):把元素 x 和元素 y 所在的集合合并,要求 x 和 y 所在的集合不相交,如果相交則不合并。
find(x):找到元素 x 所在的集合的代表,該操作也可以用于判斷兩個元素是否位于同一個集合,只要將它們各自的代表比較一下就可以了。
package com.dataStructure.union_find;
// 我們的第五版Union-Find
public class UnionFind5 {
// rank[i]表示以i為根的集合所表示的樹的層數
// 在后續的代碼中, 我們并不會維護rank的語意, 也就是rank的值在路徑壓縮的過程中, 有可能不在是樹的層數值
// 這也是我們的rank不叫height或者depth的原因, 他只是作為比較的一個標準
private int[] rank;
private int[] parent; // parent[i]表示第i個元素所指向的父節點
private int count; // 數據個數
// 構造函數
public UnionFind5(int count){
rank = new int[count];
parent = new int[count];
this.count = count;
// 初始化, 每一個parent[i]指向自己, 表示每一個元素自己自成一個集合
for( int i = 0 ; i < count ; i ++ ){
parent[i] = i;
rank[i] = 1;
}
}
// 查找過程, 查找元素p所對應的集合編號
// O(h)復雜度, h為樹的高度
private int find(int p){
assert( p >= 0 && p < count );
// path compression 1
while( p != parent[p] ){
parent[p] = parent[parent[p]];
p = parent[p];
}
return p;
// path compression 2, 遞歸算法
// if( p != parent[p] )
// parent[p] = find( parent[p] );
// return parent[p];
}
// 查看元素p和元素q是否所屬一個集合
// O(h)復雜度, h為樹的高度
public boolean isConnected( int p , int q ){
return find(p) == find(q);
}
// 合并元素p和元素q所屬的集合
// O(h)復雜度, h為樹的高度
public void unionElements(int p, int q){
int pRoot = find(p);
int qRoot = find(q);
if( pRoot == qRoot )
return;
// 根據兩個元素所在樹的元素個數不同判斷合并方向
// 將元素個數少的集合合并到元素個數多的集合上
if( rank[pRoot] < rank[qRoot] ){
parent[pRoot] = qRoot;
}
else if( rank[qRoot] < rank[pRoot]){
parent[qRoot] = pRoot;
}
else{ // rank[pRoot] == rank[qRoot]
parent[pRoot] = qRoot;
rank[qRoot] += 1; // 此時, 我維護rank的值
}
}
}
總結
以上就是本文關于java編程實現并查集的路徑壓縮代碼詳解的全部內容,希望對大家有所幫助。感興趣的朋友可以繼續參閱本站其他相關專題,如有不足之處,歡迎留言指出。感謝朋友們對本站的支持!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。