您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本文研究的主要是Java編程數組中最大子矩陣的相關內容,具體介紹如下。
遇到一個好人,可以改變一生;遇到一本好書,又何嘗不是呢?
最近在翻閱 左程云先生的《程序員代碼面試指南–IT名企算法與數據結構題目最優解》時就非常的有感悟。建議有這方面愛好的博友,也去觀摩觀摩。
書中講解的基于棧的數組的最大矩陣的算法很經典,但是博主能力有限,沒能徹底的領悟該算法的精髓,但是根據這個思想,博主想出了一種簡易的應對該類問題的算法,現概述如下。
核心思想
先來看一張圖吧,我們就可以大致的理解了。

如圖,每一個輪次都是一次運算,而我們的核心就是針對這每一個輪次的內部的運算。
計算出每一層連續不間斷的最大長度
也就是說,我們是最這個數組進行由下至上的輪次計算,然后針對每一輪就可以計算出本輪次可以得出的連續最大子矩陣的面積。然后只需要比較每一個輪次的最大的那個數據,返回就可以求出該數組最大的連續的子矩陣的面積了。
代碼
好了,有了上面的核心思想的鋪墊,我們就可以著手編寫代碼了。(雖然我也覺得自己并沒有說的很清楚,見諒見諒)。
package stack_and_queue;
/**
* @author 郭 璞<br>
* 根據數組來計算連續的最大的矩形區域的面積
*/
public class MaxRectangle {
public static void main(String[] args) {
Integer[] arr = { 2, 1, 3, 5, 7, 6, 4 };
Integer maxRectangle = maxRectangleArea(arr);
System.out.println("數組中最大的連續的矩形區域的面積為: " + maxRectangle);
}
/**
* @param arr
* @return 數組中連續矩形區域的最大面積
*/
private static Integer maxRectangleArea(Integer[] arr) {
int[] result = new int[arr.length];
// 對數組進行遍歷式的計算,由底向上不間斷的連續長度
for (int i = 1; i <= arr.length; i++) {
// 當前輪次 中實現對連續長度的累加的臨時取值
int templen = 0;
// 記錄本輪高度下的最大連續長度
int templen_max = 0;
// 內層循環應該是從數組首部開始,而從當先層下標開始會導致前面部分數據的丟失
for (int j = 1; j <= arr.length; j++) {
if (arr[j - 1] >= i) {
templen += 1;
templen_max = templen;
} else {
templen = 0;
}
}
result[i - 1] = i * templen_max;
// System.out.println("第" + i + "層連續不間斷的最大長度為:" + templen_max);
}
// 求得結果集數組中數值最大的那個數,即為所求連續區域中的最大的矩形域的面積
int maxArea = 0;
for (int i = 0; i < result.length; i++) {
maxArea = maxArea > result[i] ? maxArea : result[i];
}
// 將所求得的最大連續矩形域的面積返回
return maxArea;
}
}
代碼中的注釋也比較的全面,就不再過多的贅述了。
測試
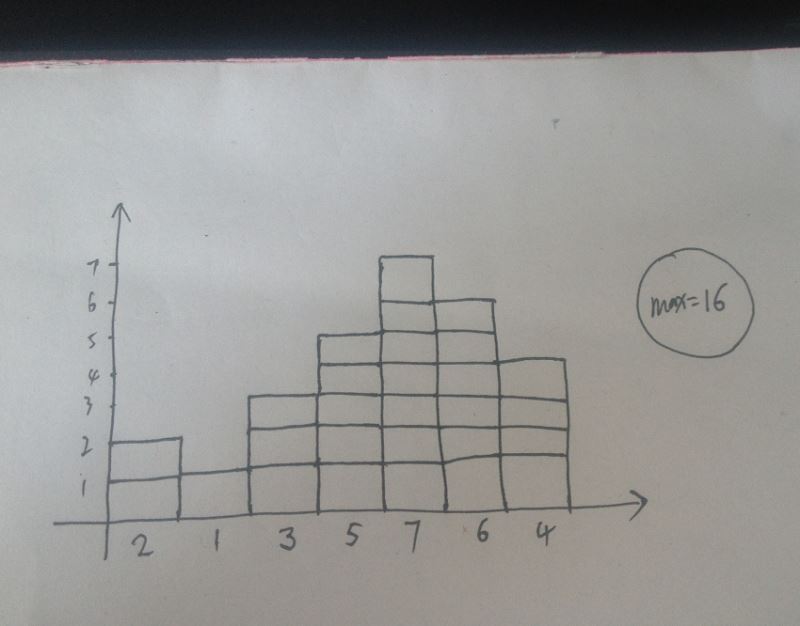
下面就對數組進行測試。首先以本文開頭圖片上所示的數組來進行測試吧。
Integer[] arr = {2,1,3,5,7,6,4}
···
數組中最大的連續的矩形區域的面積為: 16
然后我們修改一下數組中元素的值,來進一步的測試看看結果是否正確。
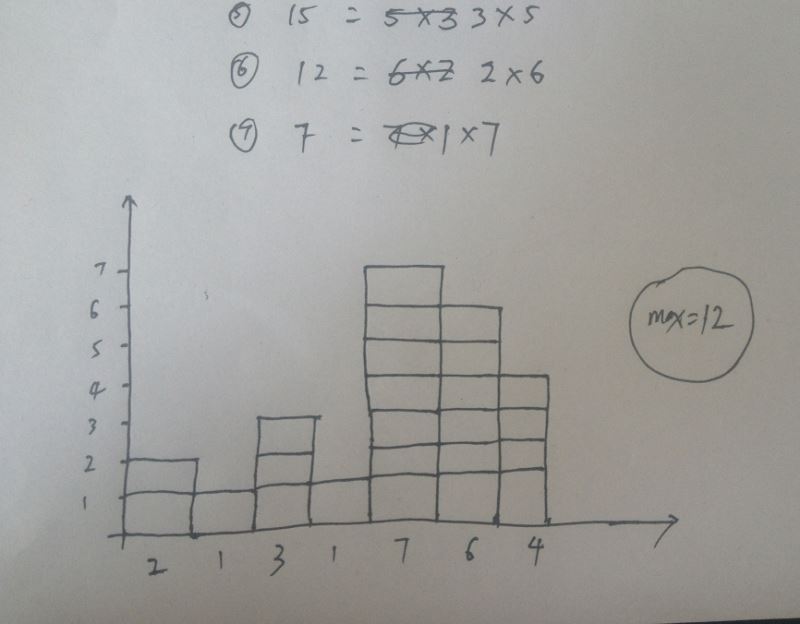
Integer[] arr = {2,1,3,1,7,6,4}
···
數組中最大的連續的矩形區域的面積為: 12
經博主本人親自測試,該算法可以正常的工作。 :)
優化部分
說道優化部分,首先我們可以看出的估計便是最后的那步求結果集數組中的最大值了吧。
確實是的,我們其實可以另外申請一個變量,來記錄到目前為止的輪次的最大的那個子矩陣的面積的。不過 這點優化而言起到的作用不是很大,時間復雜度也沒有什么比較大的改善。
另外一點,我覺的可以比較好的切入點就是對每一個輪次的進行運算的時候添加一個判斷,來決定當前輪次之前是否往下循環。如果數組中的元素的波動比較大的話,優化的程度還是很不錯的。
總結
這個小算法比較精巧,唯一比較缺憾的地方就是時間復雜度稍微的有點大了。如果讀者在尋求一種時間復雜度比較小的算法的話,請繞道咯。
如果只是想尋求一個結果,還是不錯的。至少比暴力方式的計算效率高多了。
以上就是本文關于Java編程數組中最大子矩陣簡便解法實現代碼的全部內容,希望對大家有所幫助。感興趣的朋友可以繼續參閱本站其他相關專題,如有不足之處,歡迎留言指出。感謝朋友們對本站的支持!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。