Java鏈表中元素刪除的實現方法詳解【只刪除一個元素情況】

本文實例講述了Java鏈表中元素刪除的實現方法。分享給大家供大家參考，具體如下：

該部分與上一節是息息相關的，關于如何在鏈表中刪除元素，我們一步一步來分析：

一、圖示刪除邏輯

假設我們需要在鏈表中刪除索引為2位置的元素，此時鏈表結構為：

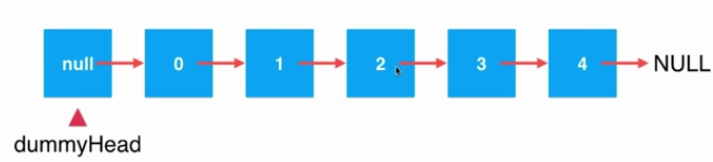
若要刪除索引為2位置的元素，需要獲取索引為2位置的元素之前的前置節點（此時為索引為1的位置的元素），因此我們需要設計一個變量prev來記錄前置節點。

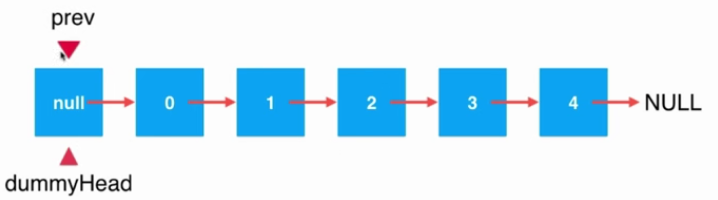
1.初始時變量prev指向虛擬頭結點dummyHead:

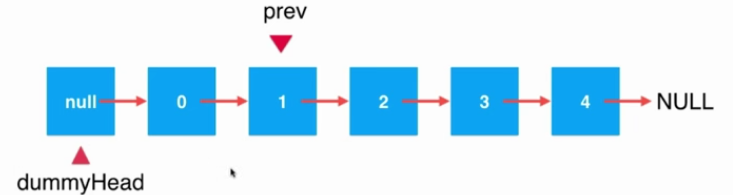
2.尋找到前置節點位置，（對于該例子前置節點為索引為1的位置的元素）。

則此時prev記錄的next即為需要刪除的節點，記為delNode變量。

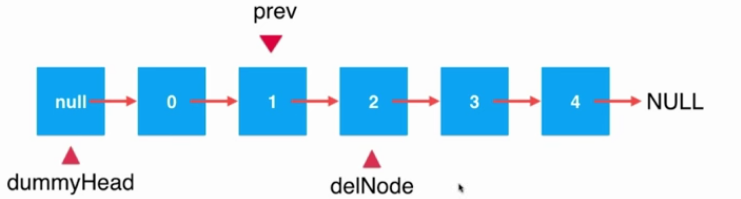
3.刪除操作

第一步：將prev的next指向delNode的next,如圖：

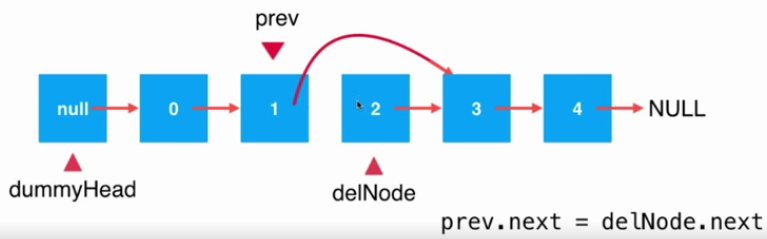
代碼為：

prev.next=delNode.next;

 第二步：為了java能夠回收這個被刪除的空間，我們手動讓需要被刪除的節點從鏈表中脫離開來，也就是delNode的next變為null。

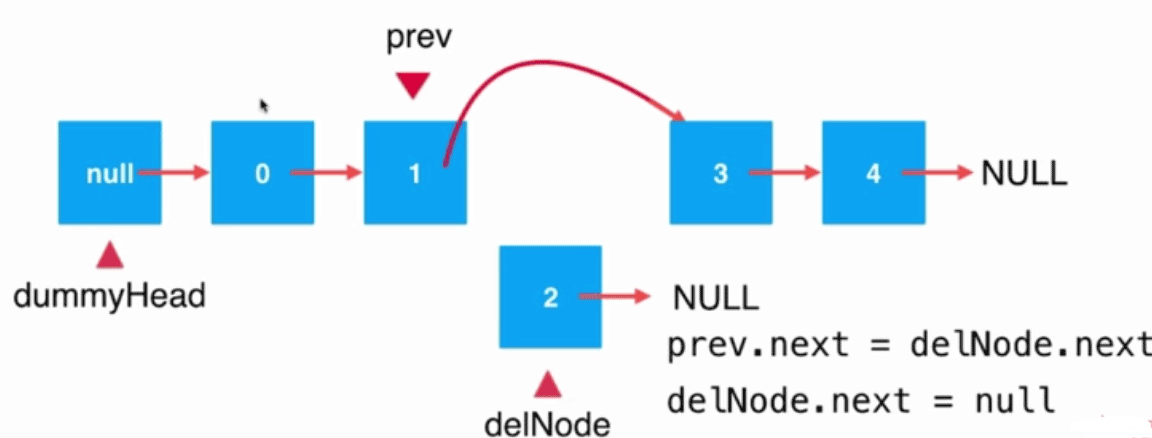
代碼為：

delNode.next=null;

二、代碼實現刪除邏輯

2.1 從鏈表刪除第index（0-based）個位置的元素 ，返回刪除的元素

首先，初始化當前前置節點指向虛擬頭結點，然后遍歷尋找到需要被刪除節點的前置節點，最后執行刪除邏輯。

//從鏈表刪除第index（0-based）個位置的元素 ，返回刪除的元素 (實際不常用，練習用)
  public E remove(int index) {
    if (index < 0 || index >= size) {
      throw new IllegalArgumentException("remove failed,Illegal index");
    }

    //獲取虛擬頭節點
    Node<E> prev = dummyHead;
    for (int i = 0; i < index; i++) {
      //獲取到刪除元素之前節點
      prev = prev.next;
    }

    Node<E> retNode = prev.next;//被刪除的元素
    prev.next = retNode.next;
    retNode.next = null;
    size--;

    return retNode.e;
  }

2.2 從鏈表中刪除第一個元素，返回刪除的元素

基于remove(int index)方法實現該方法：

//從鏈表中刪除第一個元素，返回刪除的元素
  public E removeFirst() {
    return remove(0);
  }

2.3 從鏈表中刪除最后一個元素，返回刪除的元素

基于remove(int index)方法實現該方法：

//從鏈表中刪除最后一個元素，返回刪除的元素
  public E removeLast() {
    return remove(size - 1);
  }

三、測試刪除邏輯

基于上一節的測試代碼，我們新增刪除邏輯代碼，此時貼出全部測試代碼：

package LinkedList;

public class TestMain {
  public static void main(String[] args) {
    LinkedList<Integer> linkedList = new LinkedList<Integer>();

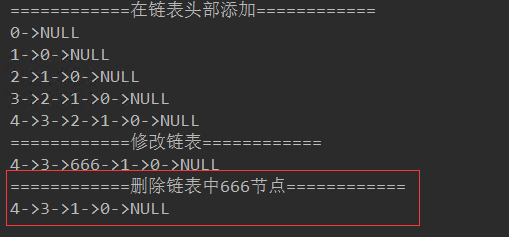
    System.out.println("============在鏈表頭部添加============");
    for (int i = 0; i < 5; i++) {
      linkedList.addFirst(i);
      System.out.println(linkedList);
    }

    System.out.println("============修改鏈表============");
    linkedList.set(2, 666);
    System.out.println(linkedList);

    System.out.println("============刪除鏈表中666節點============");
    linkedList.remove(2);
    System.out.println(linkedList);
  }
}

結果為：

 四、鏈表的時間復雜度分析

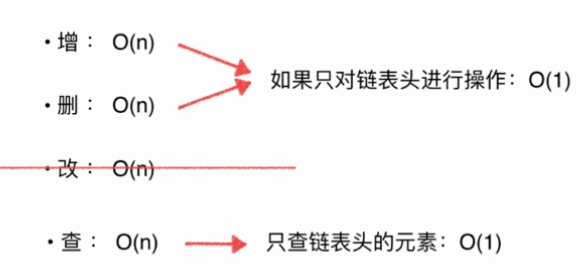
4.1 添加操作的時間復雜度

（1）在鏈表尾部添加（addLast()）需要從頭遍歷，時間復雜度為O(n);

（2）在鏈表頭部添加（addFirst()），時間復雜度為O(1);

（3）在鏈表任意位置添加(add(int index,E e))，平均情況下為O(n/2)=O(n);

4.2 刪除操作的時間復雜度

（1）刪除鏈表最后一個元素(removeLast())，需要遍歷找到最后元素的前一個元素，故時間復雜度為O(n);

（2）刪除鏈表的第一個元素(removeFirst()),時間復雜度為O(1)

（3）刪除鏈表中任意位置節點(remove(index)),平均情況下時間復雜度為O(n/2)=O(n);

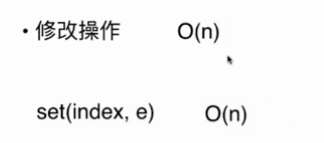
 4.3 修改操作

由于鏈表不支持隨機訪問，需要從頭開始尋找直到找到需要修改的節點，故時間復雜度為O(n)

4.4 查找操作

由于鏈表不支持隨機訪問，需要從頭開始尋找直到找到需要的節點，故時間復雜度為O(n)

 從上不難看出，關于鏈表的添加操作、刪除操作、修改操作、查找操作的時間復雜度均為O(n),看到這個頓時心涼了半截，這個還搞個mao,還不如數組呢，其實確實是這樣的，因為對于數組來說，只要有索引即可實現快速訪問。但是對于鏈表來說，我們如果只對鏈表頭進行添加操作、刪除操作、查找操作那么它的的時間復雜度為均O(1),這時和數組是一樣，是動態的，不會大量的浪費內存空間，這就是它的優勢，由于鏈表是最基礎的動態數據結構，在此基礎上將會有更多關于鏈表的應用。

關于本小節，若您覺得還行、還過得去，麻煩給個推薦吧，謝謝！！

關于鏈表的源碼  https://github.com/FelixBin/dataStructure/tree/master/src/LinkedList

更多關于java算法相關內容感興趣的讀者可查看本站專題：《Java數據結構與算法教程》、《Java操作DOM節點技巧總結》、《Java文件與目錄操作技巧匯總》和《Java緩存操作技巧匯總》

希望本文所述對大家java程序設計有所幫助。