您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家分享的是有關JavaScript程序設計高級算法之動態規劃的示例分析的內容。小編覺得挺實用的,因此分享給大家做個參考,一起跟隨小編過來看看吧。
具體如下:
其實像在我們前端的開發中,用到的高級算法并不多,大部分情況if語句,for語句,swith語句等等,就可以解決了。稍微復雜的,可能會想到用遞歸去的解決。
但要注意的是遞歸寫起來簡潔,但實際上執行的效率并不高。
我們再看看動態規劃的算法:
動態規劃解決方案從底部開始解決問題, 將所有小問題解決掉, 然后合并成一個整體解決方案, 從而解決掉整個大問題 。
實例舉例 (計算斐波那契數列)
斐波那契數列指的是這樣一個數列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368........
這個數列從第3項開始,每一項都等于前兩項之和。
針對這個數列,可以用一個遞歸的函數去計算第n項 數值
// 斐波那契數列
function recurFib(n) {
if(n < 2){
return n ;
}else {
// document.write("第"+(n-1)+"次計算 n-1="+(n-1)+recurFib(n-1)+' ');
// document.write("n-2="+(n-2)+recurFib(n-2)+"<br>");
return recurFib(n-1)+recurFib(n-2)
}
}確實是個非常簡潔的代碼,上面有被注釋的代碼 ,是用來打印出當n=多少,要執行多少次函數,不過明眼人一眼就能看出來執行的次數隨著n的變大,次數也會非常恐怖增長。
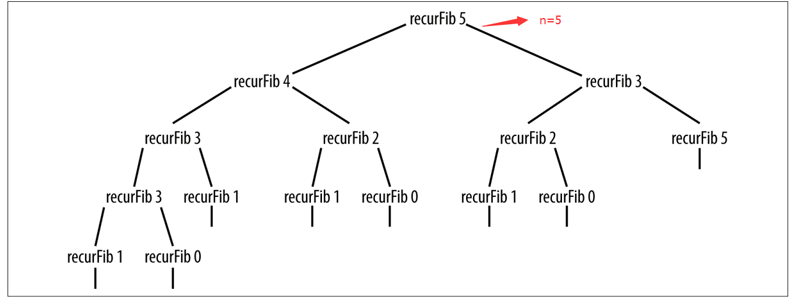
當n=5的時候,遞歸樹已經長的很大了……可以預見當n=10,甚至n=100的時候……
明白了遞歸函數執行效率之差,我們再來看的動態規劃是如何做的
function dynFib(n) {
let val = [];
for(let i = 0; i <= n; ++i){
val[i]=0;
}
if(n ===1 || n === 2){
return 1;
}
else {
val[1] =1;
val[2] = 2;
for(let i = 3; i <= n; ++i){
val[i] = val [i-1] +val[i-2] ;
}
}
return val[n-1]
}通過數組 val 中保存了中間結果, 如果要計算的斐波那契數是 1 或者 2, 那么 if 語句會返回 1。 否則,數值 1 和 2 將被保存在 val 數組中 1 和 2 的位置。
循環將會從 3 到輸入的參數之間進行遍歷, 將數組的每個元素賦值為前兩個元素之和, 循環結束, 數組的最后一個元素值即為最終計算得到的斐波那契數值, 這個數值也將作為函數的返回值。
接下來可以寫個簡單的測試函數,來對比兩者的運行時間。
// 定義一個測試函數,將待測函數作為參數傳入
function test(func,n){
let start = new Date().getTime();//起始時間
let res = func(n);//執行待測函數
document.write('<br>'+'當n='+n+'的時候 '+res+'<br>');
let end = new Date().getTime();//結束時間
return (end - start)+"ms";//返回函數執行需要時間
}打印函數執行
let time = test(recurFib,40); document.write(time); let time2 = test(dynFib,40); document.write(time2);
結果如下:

最后, 你或許已經意識到在使用迭代的方案計算斐波那契數列時, 是可以不使用數組的。
需要用到數組的原因是因為動態規劃算法通常需要將中間結果保存起來。
以下是迭代版本的斐波那契函數義
function iterFib(n) {
let last = 1;
let nextLast = 1;
let result = 1;
for (let i = 2; i < n; ++i) {
result = last + nextLast;
nextLast = last;
last = result;
}
return result;
}當然這個迭代版本的與數組的版本的效率也是相同的。

感謝各位的閱讀!關于“JavaScript程序設計高級算法之動態規劃的示例分析”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,讓大家可以學到更多知識,如果覺得文章不錯,可以把它分享出去讓更多的人看到吧!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。