您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
一、概述
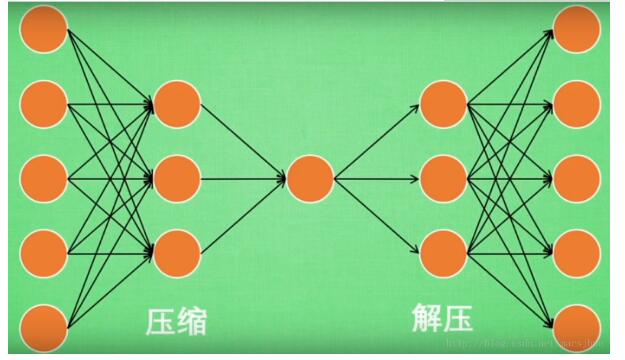
AutoEncoder大致是一個將數據的高維特征進行壓縮降維編碼,再經過相反的解碼過程的一種學習方法。學習過程中通過解碼得到的最終結果與原數據進行比較,通過修正權重偏置參數降低損失函數,不斷提高對原數據的復原能力。學習完成后,前半段的編碼過程得到結果即可代表原數據的低維“特征值”。通過學習得到的自編碼器模型可以實現將高維數據壓縮至所期望的維度,原理與PCA相似。
二、模型實現
1. AutoEncoder
首先在MNIST數據集上,實現特征壓縮和特征解壓并可視化比較解壓后的數據與原數據的對照。
先看代碼:
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
# 導入MNIST數據
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=False)
learning_rate = 0.01
training_epochs = 10
batch_size = 256
display_step = 1
examples_to_show = 10
n_input = 784
# tf Graph input (only pictures)
X = tf.placeholder("float", [None, n_input])
# 用字典的方式存儲各隱藏層的參數
n_hidden_1 = 256 # 第一編碼層神經元個數
n_hidden_2 = 128 # 第二編碼層神經元個數
# 權重和偏置的變化在編碼層和解碼層順序是相逆的
# 權重參數矩陣維度是每層的 輸入*輸出,偏置參數維度取決于輸出層的單元數
weights = {
'encoder_h2': tf.Variable(tf.random_normal([n_input, n_hidden_1])),
'encoder_h3': tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2])),
'decoder_h2': tf.Variable(tf.random_normal([n_hidden_2, n_hidden_1])),
'decoder_h3': tf.Variable(tf.random_normal([n_hidden_1, n_input])),
}
biases = {
'encoder_b1': tf.Variable(tf.random_normal([n_hidden_1])),
'encoder_b2': tf.Variable(tf.random_normal([n_hidden_2])),
'decoder_b1': tf.Variable(tf.random_normal([n_hidden_1])),
'decoder_b2': tf.Variable(tf.random_normal([n_input])),
}
# 每一層結構都是 xW + b
# 構建編碼器
def encoder(x):
layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['encoder_h2']),
biases['encoder_b1']))
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['encoder_h3']),
biases['encoder_b2']))
return layer_2
# 構建解碼器
def decoder(x):
layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['decoder_h2']),
biases['decoder_b1']))
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['decoder_h3']),
biases['decoder_b2']))
return layer_2
# 構建模型
encoder_op = encoder(X)
decoder_op = decoder(encoder_op)
# 預測
y_pred = decoder_op
y_true = X
# 定義代價函數和優化器
cost = tf.reduce_mean(tf.pow(y_true - y_pred, 2)) #最小二乘法
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)
with tf.Session() as sess:
# tf.initialize_all_variables() no long valid from
# 2017-03-02 if using tensorflow >= 0.12
if int((tf.__version__).split('.')[1]) < 12 and int((tf.__version__).split('.')[0]) < 1:
init = tf.initialize_all_variables()
else:
init = tf.global_variables_initializer()
sess.run(init)
# 首先計算總批數,保證每次循環訓練集中的每個樣本都參與訓練,不同于批量訓練
total_batch = int(mnist.train.num_examples/batch_size) #總批數
for epoch in range(training_epochs):
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size) # max(x) = 1, min(x) = 0
# Run optimization op (backprop) and cost op (to get loss value)
_, c = sess.run([optimizer, cost], feed_dict={X: batch_xs})
if epoch % display_step == 0:
print("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(c))
print("Optimization Finished!")
encode_decode = sess.run(
y_pred, feed_dict={X: mnist.test.images[:examples_to_show]})
f, a = plt.subplots(2, 10, figsize=(10, 2))
for i in range(examples_to_show):
a[0][i].imshow(np.reshape(mnist.test.images[i], (28, 28)))
a[1][i].imshow(np.reshape(encode_decode[i], (28, 28)))
plt.show()
代碼解讀:
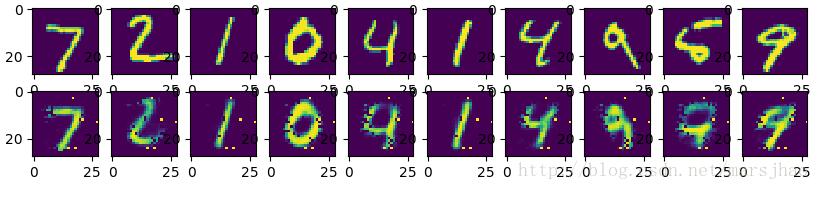
首先,導入將要使用到的各種庫和數據集,定義各個參數如學習率、訓練迭代次數等,清晰明了便于后期修改。由于自編碼器的神經網絡結構非常有規律性,都是xW + b的結構,故將每一層的權重W和偏置b的變量tf.Variable統一置于一個字典中,通過字典的key值更加清晰明了的描述。模型構建思路上,將編碼器部分和解碼器部分分開構建,每一層的激活函數使用Sigmoid函數,編碼器通常與編碼器使用同樣的激活函數。通常編碼器部分和解碼器部分是一個互逆的過程,例如我們設計將784維降至256維再降至128維的編碼器,解碼器對應的就是從128維解碼至256維再解碼至784維。定義代價函數,代價函數表示為解碼器的輸出與原始輸入的最小二乘法表達,優化器采用AdamOptimizer訓練階段每次循環將所有的訓練數據都參與訓練。經過訓練,最終將訓練結果與原數據可視化進行對照,如下圖,還原度較高。如果增大訓練循環次數或者增加自編碼器的層數,可以得到更好的還原效果。
運行結果:
2. Encoder
Encoder編碼器工作原理與AutoEncoder相同,我們將編碼得到的低維“特征值”在低維空間中可視化出來,直觀顯示數據的聚類效果。具體地說,將784維的MNIST數據一步步的從784到128到64到10最后降至2維,在2維坐標系中展示遇上一個例子不同的是,在編碼器的最后一層中我們不采用Sigmoid激活函數,而是將采用默認的線性激活函數,使輸出為(-∞,+∞)。
完整代碼:
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("MNIST_data/", one_hot=False)
learning_rate = 0.01
training_epochs = 10
batch_size = 256
display_step = 1
n_input = 784
X = tf.placeholder("float", [None, n_input])
n_hidden_1 = 128
n_hidden_2 = 64
n_hidden_3 = 10
n_hidden_4 = 2
weights = {
'encoder_h2': tf.Variable(tf.truncated_normal([n_input, n_hidden_1],)),
'encoder_h3': tf.Variable(tf.truncated_normal([n_hidden_1, n_hidden_2],)),
'encoder_h4': tf.Variable(tf.truncated_normal([n_hidden_2, n_hidden_3],)),
'encoder_h5': tf.Variable(tf.truncated_normal([n_hidden_3, n_hidden_4],)),
'decoder_h2': tf.Variable(tf.truncated_normal([n_hidden_4, n_hidden_3],)),
'decoder_h3': tf.Variable(tf.truncated_normal([n_hidden_3, n_hidden_2],)),
'decoder_h4': tf.Variable(tf.truncated_normal([n_hidden_2, n_hidden_1],)),
'decoder_h5': tf.Variable(tf.truncated_normal([n_hidden_1, n_input],)),
}
biases = {
'encoder_b1': tf.Variable(tf.random_normal([n_hidden_1])),
'encoder_b2': tf.Variable(tf.random_normal([n_hidden_2])),
'encoder_b3': tf.Variable(tf.random_normal([n_hidden_3])),
'encoder_b4': tf.Variable(tf.random_normal([n_hidden_4])),
'decoder_b1': tf.Variable(tf.random_normal([n_hidden_3])),
'decoder_b2': tf.Variable(tf.random_normal([n_hidden_2])),
'decoder_b3': tf.Variable(tf.random_normal([n_hidden_1])),
'decoder_b4': tf.Variable(tf.random_normal([n_input])),
}
def encoder(x):
layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['encoder_h2']),
biases['encoder_b1']))
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['encoder_h3']),
biases['encoder_b2']))
layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, weights['encoder_h4']),
biases['encoder_b3']))
# 為了便于編碼層的輸出,編碼層隨后一層不使用激活函數
layer_4 = tf.add(tf.matmul(layer_3, weights['encoder_h5']),
biases['encoder_b4'])
return layer_4
def decoder(x):
layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, weights['decoder_h2']),
biases['decoder_b1']))
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, weights['decoder_h3']),
biases['decoder_b2']))
layer_3 = tf.nn.sigmoid(tf.add(tf.matmul(layer_2, weights['decoder_h4']),
biases['decoder_b3']))
layer_4 = tf.nn.sigmoid(tf.add(tf.matmul(layer_3, weights['decoder_h5']),
biases['decoder_b4']))
return layer_4
encoder_op = encoder(X)
decoder_op = decoder(encoder_op)
y_pred = decoder_op
y_true = X
cost = tf.reduce_mean(tf.pow(y_true - y_pred, 2))
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)
with tf.Session() as sess:
# tf.initialize_all_variables() no long valid from
# 2017-03-02 if using tensorflow >= 0.12
if int((tf.__version__).split('.')[1]) < 12 and int((tf.__version__).split('.')[0]) < 1:
init = tf.initialize_all_variables()
else:
init = tf.global_variables_initializer()
sess.run(init)
total_batch = int(mnist.train.num_examples/batch_size)
for epoch in range(training_epochs):
for i in range(total_batch):
batch_xs, batch_ys = mnist.train.next_batch(batch_size) # max(x) = 1, min(x) = 0
_, c = sess.run([optimizer, cost], feed_dict={X: batch_xs})
if epoch % display_step == 0:
print("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(c))
print("Optimization Finished!")
encoder_result = sess.run(encoder_op, feed_dict={X: mnist.test.images})
plt.scatter(encoder_result[:, 0], encoder_result[:, 1], c=mnist.test.labels)
plt.colorbar()
plt.show()
實驗結果:
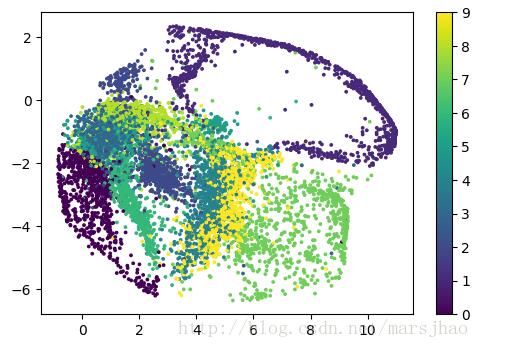
由結果可知,2維編碼特征有較好的聚類效果,圖中每個顏色代表了一個數字,聚集性很好。
當然,本次實驗所得到的結果只是對AutoEncoder做一個簡單的介紹,要想得到期望的效果,還應該設計更加復雜的自編碼器結構,得到區分性更好的特征。
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。