您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
ARIMA模型
ARIMA模型的全稱是自回歸移動平均模型,是用來預測時間序列的一種常用的統計模型,一般記作ARIMA(p,d,q)。
ARIMA的適應情況
ARIMA模型相對來說比較簡單易用。在應用ARIMA模型時,要保證以下幾點:
判斷時序數據穩定
基本判斷方法:穩定的數據,總體上是沒有上升和下降的趨勢的,是沒有周期性的,方差趨向于一個穩定的值。
ARIMA數學表達
ARIMA(p,d,q),其中p是數據本身的滯后數,是AR模型即自回歸模型中的參數。d是時間序列數據需要幾次差分才能得到穩定的數據。q是預測誤差的滯后數,是MA模型即滑動平均模型中的參數。
a) p參數與AR模型
AR模型描述的是當前值與歷史值之間的關系,滯后p階的AR模型可以表示為:
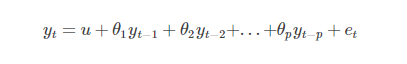
其中u是常數,et代表誤差。
b) q參數與MA模型
MA模型描述的是當前值與自回歸部分的誤差累計的關系,滯后q階的MA模型可以表示為:
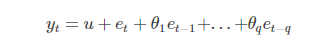
其中u是常數,et代表誤差。
c) d參數與差分
一階差分:
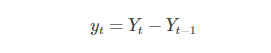
二階差分:
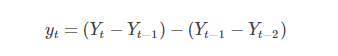
d) ARIMA = AR+MA
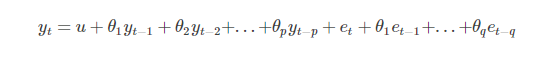
ARIMA模型使用步驟

Python調用ARIMA
#差分處理 diff_series = diff_series.diff(1)#一階 diff_series2 = diff_series.diff(1)#二階 #ACF與PACF #從scipy導入包 from scipy import stats import statsmodels.api as sm #畫出acf和pacf sm.graphics.tsa.plot_acf(diff_series) sm.graphics.tsa.plot_pacf(diff_series) #arima模型 from statsmodels.tsa.arima_model import ARIMA model = ARIMA(train_data,order=(p,d,q),freq='')#freq是頻率,根據數據填寫 arima = model.fit()#訓練 print(arima) pred = arima.predict(start='',end='')#預測
總結
以上就是這篇文章的全部內容了,希望本文的內容對大家的學習或者工作具有一定的參考學習價值,謝謝大家對億速云的支持。如果你想了解更多相關內容請查看下面相關鏈接
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。