您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
線性回歸在整個財務中廣泛應用于眾多應用程序中。在之前的教程中,我們使用普通最小二乘法(OLS)計算了公司的beta與相對索引的比較。現在,我們將使用線性回歸來估計股票價格。
線性回歸是一種用于模擬因變量(y)和自變量(x)之間關系的方法。通過簡單的線性回歸,只有一個自變量x。可能有許多獨立變量屬于多元線性回歸的范疇。在這種情況下,我們只有一個自變量即日期。對于第一個日期上升到日期向量長度的整數,該日期將由1開始的整數表示,該日期可以根據時間序列數據而變化。當然,我們的因變量將是股票的價格。為了理解線性回歸,您必須了解您可能在學校早期學到的相當基本的等式。
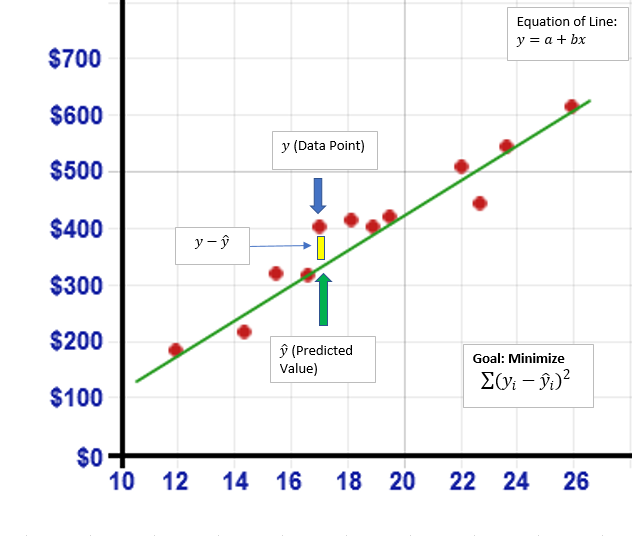
y = a + bx
從本質上講,這將構成我們對數據的最佳擬合。在OLS過程中通過數據集繪制了大量線條。該過程的目標是找到最佳擬合線,最小化平方誤差和(SSE)與股票價格(y)的實際值以及我們在數據集中所有點的預測股票價格。這由下圖表示。對于繪制的每條線,數據集中的每個點與模型輸出的相應預測值之間存在差異。將這些差異中的每一個加起來并平方以產生平方和。從列表中,我們采用最小值導致我們的最佳匹配線。考慮下圖:
第一部分:獲取數據:
from matplotlib import style
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import quandl
import datetime
style.use('ggplot')
#Dates
start_date = datetime.date(2017,1,3)
t_date=start_date, end_date=end_date, collapse="daily")
df = df.reset_index()
prices = np.reshape(prices, (len(prices), 1))
第二部分:創建一個回歸對象:
', linewidth=3, label = 'Predicted Price') #plotting the line made by linear regression
plt.title('Linear Regression | Time vs. Price')
plt.legend()
predicted_price =regressor.predict(date)
輸出:
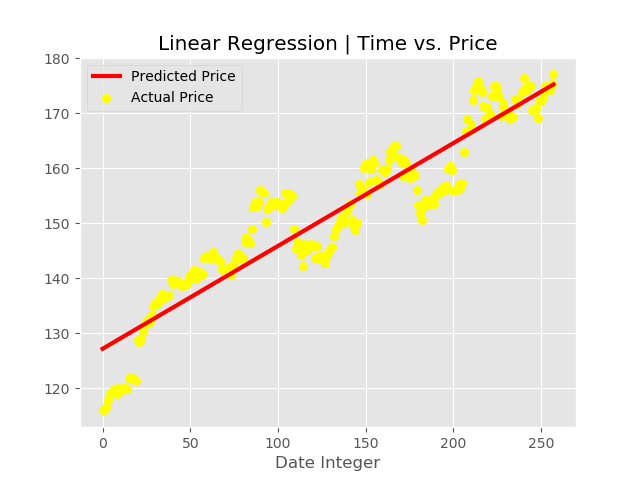
預測日期輸入價格:
創建訓練/測試集
et
xtrain, x , ytrain)
#Train
plt.title('Linear Regression | Time vs. Price')
#Test Set Graph
plt.scatter(xtest, ytest, color='yellow', label= 'Actual Price') #plotting the initial datapoints
plt.plot(xtest, regressor.predict(xtest), color='blue', linewidth=3, label = 'Predicted Price') #plotting
plt.show()
輸出:
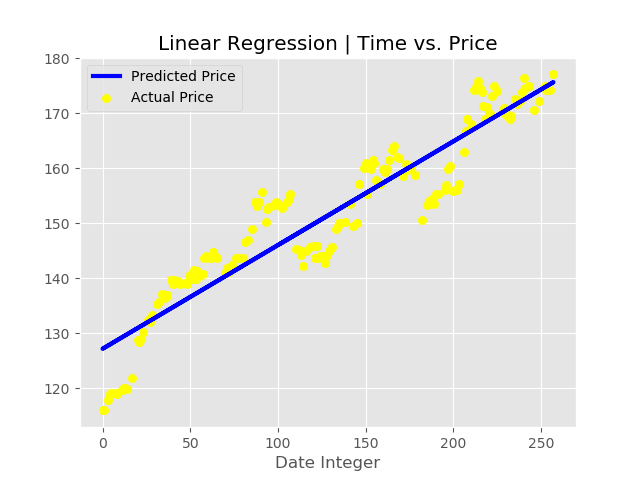
測試集:
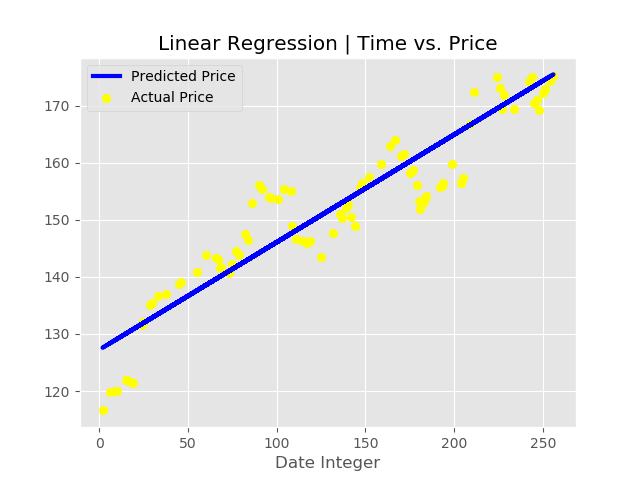
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。