溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
這篇文章將為大家詳細講解有關如何利用python實現PSO算法優化二元函數,小編覺得挺實用的,因此分享給大家做個參考,希望大家閱讀完這篇文章后可以有所收獲。
python實現PSO算法優化二元函數,具體代碼如下所示:
import numpy as np
import random
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
#----------------------PSO參數設置---------------------------------
class PSO():
def __init__(self,pN,dim,max_iter): #初始化類 設置粒子數量 位置信息維度 最大迭代次數
#self.w = 0.8
self.ws = 0.9
self.we = 0.4
self.c1 = 1.49445
self.c2 = 1.49445
self.r1= 0.6
self.r2= 0.3
self.pN = pN #粒子數量
self.dim = dim #搜索維度
self.max_iter = max_iter #迭代次數
self.X = np.zeros((self.pN,self.dim)) #所有粒子的位置(還要確定取值范圍)
self.Xmax = 5
self.Xmin = -5
self.V = np.zeros((self.pN,self.dim)) #所有粒子的速度(還要確定取值范圍)
self.Vmax = 1
self.Vmin = -1
self.pbest = np.zeros((self.pN,self.dim)) #個體經歷的最佳位置
self.gbest = np.zeros((1,self.dim)) #全局最佳位置
self.p_fit = np.zeros(self.pN) #每個個體的歷史最佳適應值
self.fit = 0 #全局最佳適應值
#---------------------目標函數Sphere函數-----------------------------
def function(self,x):
y = np.sin(10*np.pi*x)/x
return y
def Holder_table(self,x,y):
z = -np.abs(np.sin(x) * np.cos(y) * np.exp(np.abs(1 - np.sqrt(x**2 + y**2)/np.pi)))
return z
def fuck(self,x,y):
z = x**2 + y**2 - 10*np.cos(2*np.pi*x) - 10*np.cos(2*np.pi*y) + 20
return z
#---------------------初始化種群----------------------------------
def init_Population(self):
for i in range(self.pN): #遍歷所有粒子
for j in range(self.dim): #每一個粒子的緯度
self.X[i][j] = random.uniform(-5,5) #給每一個粒子的位置賦一個初始隨機值(在一定范圍內)
self.V[i][j] = random.uniform(-1,1) #給每一個粒子的速度給一個初始隨機值(在一定范圍內)
self.pbest[i] = self.X[i] #把當前粒子位置作為這個粒子的最優位置
tmp = self.fuck(self.X[i][0],self.X[i][1]) #計算這個粒子的適應度值
self.p_fit[i] = tmp #當前粒子的適應度值作為個體最優值
if(tmp > self.fit): #與當前全局最優值做比較并選取更佳的全局最優值
self.fit = tmp
self.gbest = self.X[i]
#---------------------更新粒子位置----------------------------------
def iterator(self):
fitness = []
for t in range(self.max_iter):
w = self.ws - (self.ws - self.we) * (t / self.max_iter)
for i in range(self.pN):
#更新速度
self.V[i] = w*self.V[i] + self.c1*self.r1*(self.pbest[i] - self.X[i]) + self.c2*self.r2*(self.gbest - self.X[i])
if self.V[i][0] > self.Vmax:
self.V[i][0] = self.Vmax
elif self.V[i][0] < self.Vmin:
self.V[i][0] = self.Vmin
if self.V[i][1] > self.Vmax:
self.V[i][1] = self.Vmax
elif self.V[i][1] < self.Vmin:
self.V[i][1] = self.Vmin
#更新位置
self.X[i] = self.X[i] + self.V[i]
if self.X[i][0] > self.Xmax:
self.X[i][0] = self.Xmax
elif self.X[i][0] < self.Xmin:
self.X[i][0] = self.Xmin
if self.X[i][1] > self.Xmax:
self.X[i][1] = self.Xmax
elif self.X[i][1] < self.Xmin:
self.X[i][1] = self.Xmin
for i in range(self.pN): #更新gbest\pbest
temp = self.fuck(self.X[i][0],self.X[i][1])
if(temp > self.p_fit[i]): #更新個體最優
self.pbest[i] = self.X[i]
self.p_fit[i] = temp
if(temp > self.fit): #更新全局最優
self.gbest = self.X[i]
self.fit = temp
fitness.append(self.fit)
print('最優值為:',self.fit)#輸出最優值
z1 = self.fit
print('最優位置為:',self.X[i][0],self.X[i][1])
x1 = self.X[i][0]
y1 = self.X[i][1]
return fitness, z1, x1,y1
#----------------------程序執行-----------------------
my_pso = PSO(pN=100,dim=2,max_iter=200)
my_pso.init_Population()
fitness,z1,x1,y1 = my_pso.iterator()
plt.figure(1)
plt.title("Figure1")
plt.xlabel("iterators", size=14)
plt.ylabel("fitness", size=14)
t = np.array([t for t in range(0,200)])
fitness = np.array(fitness)
plt.plot(t,fitness, color='b',linewidth=3)
plt.show()
fig = plt.figure(figsize=(15,10))
ax = Axes3D(fig)
X = np.arange(-5,5,0.1)
Y = np.arange(-5,5,0.1)
X,Y = np.meshgrid(X,Y)
def f(x,y):
return (x**2 + y**2 - 10*np.cos(2*np.pi*x) - 10*np.cos(2*np.pi*y) + 20)
ax.plot_surface(X,Y,f(X,Y),rstride=1,cstride=1,cmap= plt.get_cmap('rainbow'))
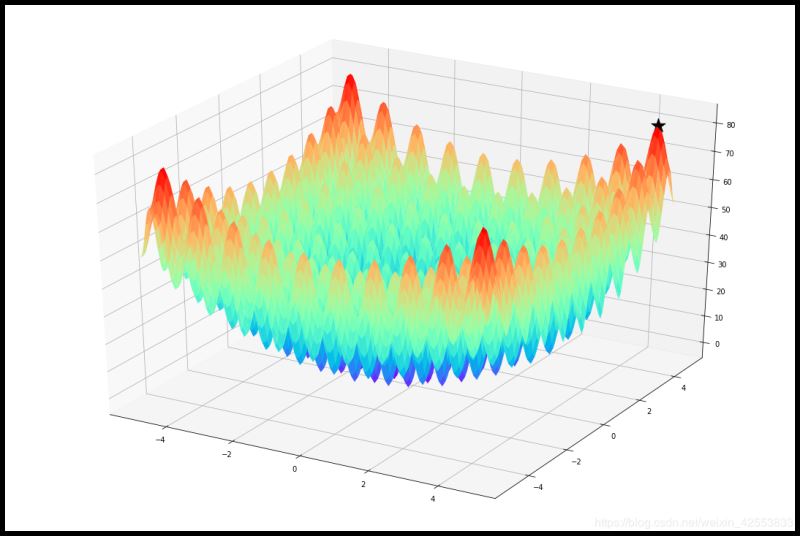
ax.scatter(x1, y1, z1,s=400,c='k',marker = '*')
plt.show()效果圖如下
關于“如何利用python實現PSO算法優化二元函數”這篇文章就分享到這里了,希望以上內容可以對大家有一定的幫助,使各位可以學到更多知識,如果覺得文章不錯,請把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。