溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
1、公式推導
對冪律分布公式:
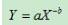
對公式兩邊同時取以10為底的對數:
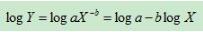

所以對于冪律公式,對X,Y取對數后,在坐標軸上為線性方程。
2、可視化
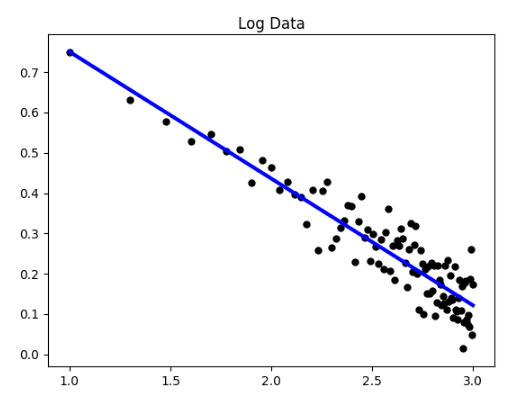
從圖形上來說,冪律分布及其擬合效果:
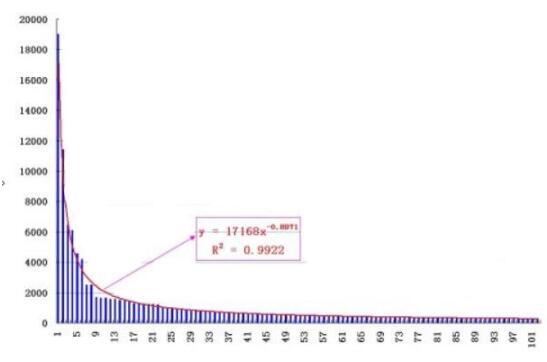
對X軸與Y軸取以10為底的對數。效果上就是X軸上1與10,與10與100的距離是一樣的。

對XY取雙對數后,坐標軸上點可以很好用直線擬合。所以,判定數據是否符合冪律分布,只需要對XY取雙對數,判斷能否用一個直線很好擬合就行。常見的直線擬合效果評估標準有擬合誤差平方和、R平方。
3、代碼實現
#!/usr/bin/env python
# -*-coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
from sklearn import linear_model
from scipy.stats import norm
def DataGenerate():
X = np.arange(10, 1010, 10) # 0-1,每隔著0.02一個數據 0處取對數,會時負無窮 生成100個數據點
noise=norm.rvs(0, size=100, scale=0.2) # 生成50個正態分布 scale=0.1控制噪聲強度
Y=[]
for i in range(len(X)):
Y.append(10.8*pow(X[i],-0.3)+noise[i]) # 得到Y=10.8*x^-0.3+noise
# plot raw data
Y=np.array(Y)
plt.title("Raw data")
plt.scatter(X, Y, color='black')
plt.show()
X=np.log10(X) # 對X,Y取雙對數
Y=np.log10(Y)
return X,Y
def DataFitAndVisualization(X,Y):
# 模型數據準備
X_parameter=[]
Y_parameter=[]
for single_square_feet ,single_price_value in zip(X,Y):
X_parameter.append([float(single_square_feet)])
Y_parameter.append(float(single_price_value))
# 模型擬合
regr = linear_model.LinearRegression()
regr.fit(X_parameter, Y_parameter)
# 模型結果與得分
print('Coefficients: \n', regr.coef_,)
print("Intercept:\n",regr.intercept_)
# The mean square error
print("Residual sum of squares: %.8f"
% np.mean((regr.predict(X_parameter) - Y_parameter) ** 2)) # 殘差平方和
# 可視化
plt.title("Log Data")
plt.scatter(X_parameter, Y_parameter, color='black')
plt.plot(X_parameter, regr.predict(X_parameter), color='blue',linewidth=3)
# plt.xticks(())
# plt.yticks(())
plt.show()
if __name__=="__main__":
X,Y=DataGenerate()
DataFitAndVisualization(X,Y)
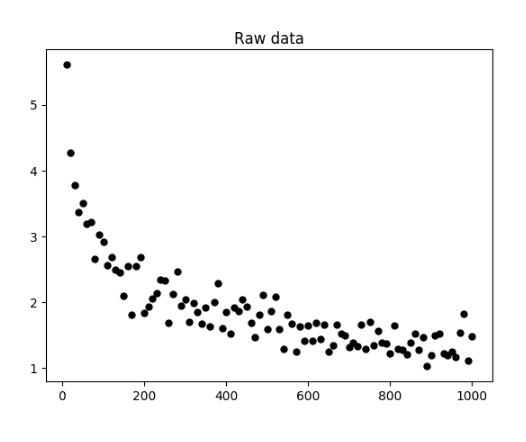
以上這篇Python數據可視化:冪律分布實例詳解就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。