您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了python如何實現圖像的離散傅立葉變換,具有一定借鑒價值,感興趣的朋友可以參考下,希望大家閱讀完這篇文章之后大有收獲,下面讓小編帶著大家一起了解一下。
圖像(MxN)的二維離散傅立葉變換可以將圖像由空間域變換到頻域中去,空間域中用x,y來表示空間坐標,頻域由u,v來表示頻率,二維離散傅立葉變換的公式如下:
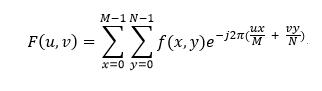
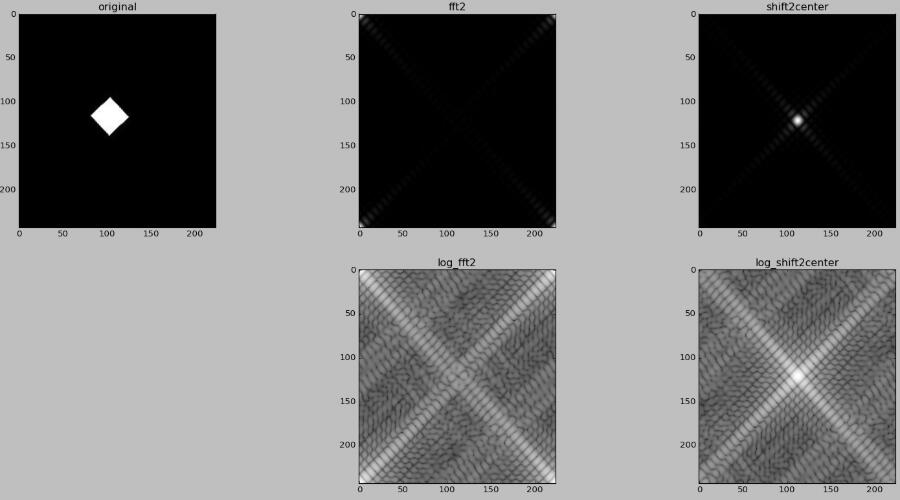
在python中,numpy庫的fft模塊有實現好了的二維離散傅立葉變換函數,函數是fft2,輸入一張灰度圖,輸出經過二維離散傅立葉變換后的結果,但是具體實現并不是直接用上述公式,而是用快速傅立葉變換。結果需要通過使用abs求絕對值才可以進行可視化,但是視覺效果并不理想,因為傅立葉頻譜范圍很大,所以要用log對數變換來改善視覺效果。
在使用log函數的時候,要寫成log(1 + x) 而不是直接用log(x),這是為了避開對0做對數處理。
另外,圖像變換的原點需要移動到頻域矩形的中心,所以要對fft2的結果使用fftshift函數。最后也可以使用log來改善可視化效果。
代碼如下:
import numpy as np
import matplotlib.pyplot as plt
img = plt.imread('photo.jpg')
#根據公式轉成灰度圖
img = 0.2126 * img[:,:,0] + 0.7152 * img[:,:,1] + 0.0722 * img[:,:,2]
#顯示原圖
plt.subplot(231),plt.imshow(img,'gray'),plt.title('original')
#進行傅立葉變換,并顯示結果
fft2 = np.fft.fft2(img)
plt.subplot(232),plt.imshow(np.abs(fft2),'gray'),plt.title('fft2')
#將圖像變換的原點移動到頻域矩形的中心,并顯示效果
shift2center = np.fft.fftshift(fft2)
plt.subplot(233),plt.imshow(np.abs(shift2center),'gray'),plt.title('shift2center')
#對傅立葉變換的結果進行對數變換,并顯示效果
log_fft2 = np.log(1 + np.abs(fft2))
plt.subplot(235),plt.imshow(log_fft2,'gray'),plt.title('log_fft2')
#對中心化后的結果進行對數變換,并顯示結果
log_shift2center = np.log(1 + np.abs(shift2center))
plt.subplot(236),plt.imshow(log_shift2center,'gray'),plt.title('log_shift2center')運行結果:

根據公式實現的二維離散傅立葉變換如下:
import numpy as np
import matplotlib.pyplot as plt
PI = 3.141591265
img = plt.imread('temp.jpg')
#根據公式轉成灰度圖
img = 0.2126 * img[:,:,0] + 0.7152 * img[:,:,1] + 0.0722 * img[:,:,2]
#顯示原圖
plt.subplot(131),plt.imshow(img,'gray'),plt.title('original')
#進行傅立葉變換,并顯示結果
fft2 = np.fft.fft2(img)
log_fft2 = np.log(1 + np.abs(fft2))
plt.subplot(132),plt.imshow(log_fft2,'gray'),plt.title('log_fft2')
h , w = img.shape
#生成一個同樣大小的復數矩陣
F = np.zeros([h,w],'complex128')
for u in range(h):
for v in range(w):
res = 0
for x in range(h):
for y in range(w):
res += img[x,y] * np.exp(-1.j * 2 * PI * (u * x / h + v * y / w))
F[u,v] = res
log_F = np.log(1 + np.abs(F))
plt.subplot(133),plt.imshow(log_F,'gray'),plt.title('log_F')直接根據公式實現復雜度很高,因為是四重循環,時間復雜度為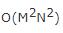 ,所以實際用的時候需要用快速傅立葉變換來實現
,所以實際用的時候需要用快速傅立葉變換來實現
感謝你能夠認真閱讀完這篇文章,希望小編分享的“python如何實現圖像的離散傅立葉變換”這篇文章對大家有幫助,同時也希望大家多多支持億速云,關注億速云行業資訊頻道,更多相關知識等著你來學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。