冒泡排序和希爾排序（三十一）

        在上節博客中，我們學習了插入排序和選擇排序，那么本次我們繼續學習冒泡排序和希爾排序。什么是冒泡排序呢？它是每次從后向前進行（假設為第 i 次），j = n - 1, n - 2, ... , i, 兩兩比較 V[j-1] 和 V[j] 的關鍵字；如果發生逆序，則交換 V[j-1] 和 V[j]。下來我們看看第 i 次冒泡排序示例，如下圖所示

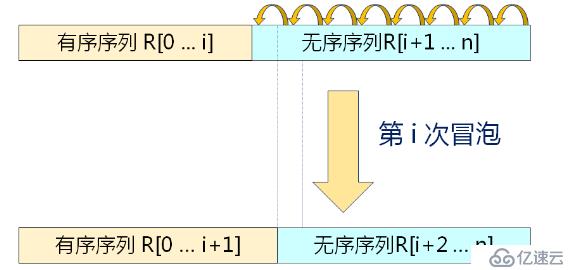
         我們來看看具體是怎么實現的，如下所示

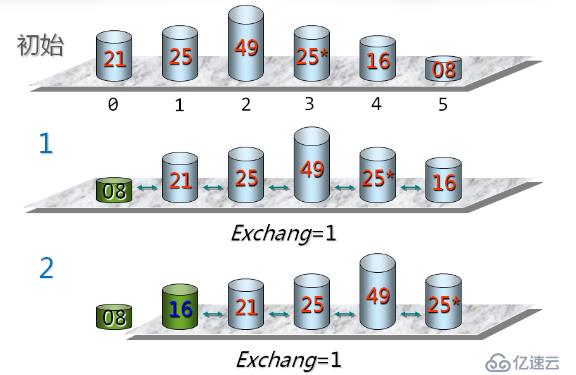
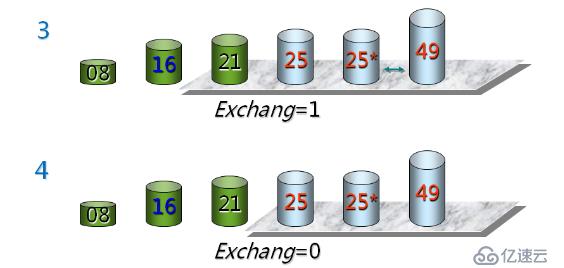
        我們看到它是兩兩比較，小的放在前面。類似于冒水泡，輕的漂浮在上面。下來我們來看看具體源碼的實現

template < typename T >
static void Bubble(T array[], int len, bool min2max = true)
{
    bool exchange = true;

    for(int i=0; (i<len) && exchange; i++)
    {
        exchange = false;

        for(int j=len-1; j>i; j--)
        {
            if( min2max ? (array[j] < array[j-1]) : (array[j] > array[j-1]) )
            {
                Swap(array[j], array[j-1]);
                exchange = true;
            }
        }
    }
}

        測試代碼如下

#include <iostream>
#include "Sort.h"

using namespace std;
using namespace DTLib;

int main()
{
    int array[] = {3, 2, 4, 1, 5};

    Sort::Bubble(array, 5);

    for(int i=0; i<5; i++)
    {
        cout << array[i] << endl;
    }
}

        我們來看看運行結果

        我們來試試在 Bubble 后面加上 false 參數，看看效果

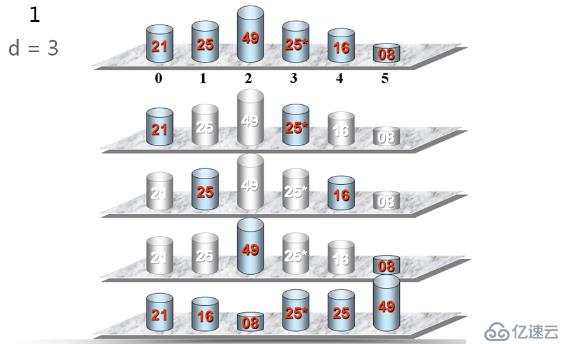
        下來我們來繼續看看希爾排序，那么它的基本思想是什么呢？將待排序列劃分為若干組，在每一組內進行插入排序，以使整個序列基本有序，然后再對整個序列進行插入排序。希爾排序示例如下

        我們來看看具體是怎么實現的，如下所示

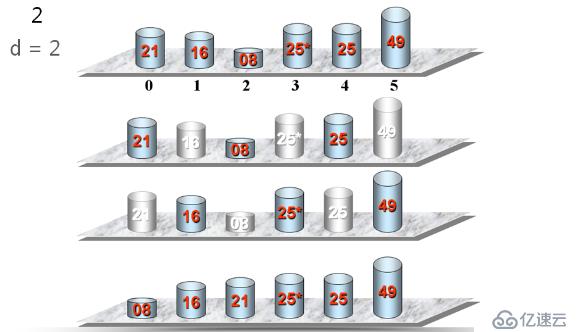
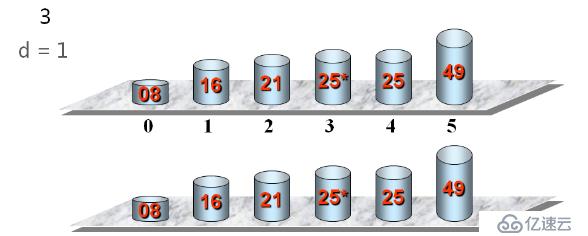
        它是利用插入排序來實現的，之所以這么實現，是因為這樣的效率比之前的幾種能高點。下來我們來看看具體源碼的實現

template < typename T >
static void Shell(T array[], int len, bool min2max = true)
{
    int d = len;

    do
    {
        d = d / 3 + 1;   // 之所以這樣寫是因為經過數學推導，這樣的效率是最高的。也可以寫成 d--;

        for(int i=d; i<len; i+=d)
        {
            int k = i;
            T e = array[i];

            for(int j=i-d; (j>=0) && (min2max ? (array[j]>e) : (array[j]<e)); j-=d)
            {
                array[j+d] = array[j];
                k = j;
            }

            if( k != i )
            {
                array[k] = e;
            }
        }
    } while( d > 1 );
}

        我們先來看看不加參數 false的效果（從小到大排序）

        再來看看從大到小的排序

        我們看到已經正確實現了。通過對冒泡排序和希爾排序的學習，總結如下：1、冒泡排序每次從后向前將較小的元素交互到位；2、冒泡排序是一種穩定的排序方法，其復雜度為O(n²)；3、希爾排序通過分組的方式進行多次插入排序，它是一種不穩定排序，其復雜度為O(n^3/2)。